внешний край дорожки отделяет площадь (6+2x)(9+2x) м^2 (это бассейн, с каждой стороны к которому прилеплен еще прямоугольник ширины х),
Эта площадь по условию равняется удвоенной площади бассейна:
(6+2x)(9+2x)=2*6*9
(3+x)(9+2x)=6*9=54
2x^2+15x+27=54
2x^2+15x-27=0
D=225+8*27=441=21^2
x=(-15+-21)/4
x=6/4=3/2 (второй корень отрицательный)
ответ: ширина дорожки 3/2 метра.
P.S. это решение некорректно, но, по-видимому, подразумевается авторами задачи. На самом деле внешний край дорожки отделяет площадь (6+2x)(9+2x)-4x^2+pi*x^2, т.к. в углах будут дуги окружностей. Но Тогда решение (в плане вычислений) будет "чуть более" трудоемким.
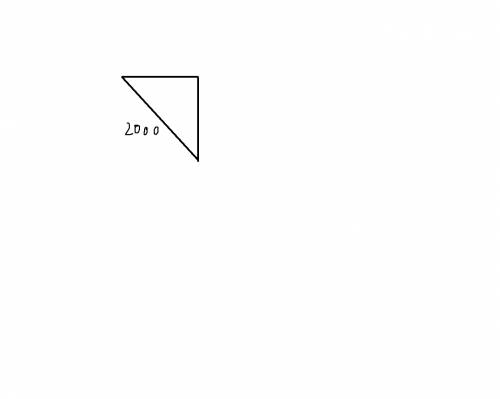
Два самолёта вылетели в двух взаимно перпендикулярных направлениях(западном и южном). Рассмотрим прямоугольный треугольник, расстояние через два часа есть гипотенуза, и она равна 2000. Найдём остальные катеты.
Пусть скорость одного из самолётов равна x, тогда скорость другого по условию равна 0.75x. Пути, пройденные самолётами за два часа и есть катеты. Они равны
2x и 1.5x.
По теореме Пифагора гипотенуза равна:
√((2x)² + (1.5x)²) = 2000
Возведём обе части уравнения в квадрат:
4x² + 2.25x² = 4000000
6.25x² = 4000000
x² = 640000
x1 = 800; x2 = -800 - этот корень не удовлетворяет условию задачи, поскольку скорость не может быть выражена отрицательным числом
Итак, 800 км/ч - скорость одного из самолётов
Скорость другого равна 800 * 0.75 = 800 * 3/4 = 200 * 3 = 600 км/ч
Задача решена
36х^2-9х-3х+1 = 0
36x^2-12x+1 = 0
D = 0
12+0/36*2 = 17/72 = 1/6
x+4^2 = 4x^2+5
2x+8 = 8x+5
2x-8x = 5-2
-6x = 3 (умножим на -1)
6x = 3
x = 0,5