Алгебра: Решите уравнение по формуле D/4

Решите уравнение по формуле D/4

👇

Увидеть ответ

Открыть все ответы

Ответ:

Chara5

17.12.2021

Правильное условие такое:

Мяч брошен вертикально вверх с начальной скоростью 24 м/с. Зависимость расстояния h (в метрах) от мяча до земли от времени полета выражается формулой h = 24t − 5t² .

Дано:

V₀=24м/с

Найти: h; t

1) Скорость - это производная от расстояния.

V = h'

V = ( 24t − 5t²)'

V = 24 - 10t

Получили формулу, которая показывает зависимость скорости V

(в м/с) от времени полета t .

2) V = 24 - 10t

V - конечная скорость, которая в момент достижения мячом наибольшей высоты равна 0.

Решим уравнение и найдем время t.

0 = 24 - 10t

10t = 24

t = 24:10

t = 2,4

t=2,4 с - время полёта мяча снизу до наибольшей высоты.

3) Находим значение наибольшей высоты, на которую поднимется мяч за t=2,4c.

h=24t-5t² при t=2,4c.

h = 24·2,4 - 5·2,4² = 2,4·(24-5·2.4) = 2,4·(24-12) = 2,4·12= 28,8 м

4) Найдем tₓ все время полета от броска с земли до момента падения его на землю

tₓ = 2t = 2 · 2,4 = 4,8c

ответ: 28,8 м; 4,8c

Объяснение:

4,6(6 оценок)

Ответ:

darialitvinenko

17.12.2021

y=x^2 - 4x + 3

а) Абсолютно никаких ограничений на аргумент здесь не накладывается. Поэтому область определения функции - все действительные числа: 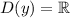$D(y) = \mathbb{R}$ .

Пункты б и в напрямую связаны друг с другом.

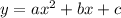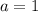Для начала посмотрим на саму нашу функцию. Она является квадратичной. Квадратичные функции имеют формулу вида y = ax^2+bx+c , где коэффициент играет большую роль - его знак определяет, ветви параболы направлены вниз или вверх. Если он положительный, то ветви направлены вверх, если отрицательный - вниз. У нашей функции y = x^2 - 4x + 3 коэффициент a = 1 . Он положительный, а значит, ветви данной параболы направлены вверх до бесконечности. Таким образом, наибольшего значения у этой функции не существует.

Чтобы найти наименьшее, для начала нужно найти координаты вершины параболы. Абсциссу находим по формуле 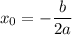$x_0 = -\dfrac{b}{2a}$ . Для нашего случая получаем:

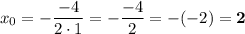
$x_0 = -\dfrac{-4}{2\cdot 1} = -\dfrac{-4}{2} = -(-2) = \bf{2}$

Чтобы найти ординату вершины параболы, подставляем в нашу функцию полученное значение абсциссы.

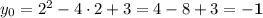$y_0 = 2^2 - 4\cdot 2 + 3 = 4 - 8 + 3 = \bf{-1}$ .

Итак, координаты вершины параболы: 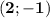$\bf{(2;-1)$ . Ордината вершины параболы, ветви которой направлены вверх, является её наименьшим значением. Делаем выводы из найденного:

б) 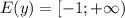$E(y) = [-1;+\infty)$ .

в) 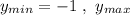$y_{min} = -1\ ,\ y_{max}$ не существует.

г) Уравнение оси симметрии параболы является абсциссой её вершины. Для нашего случая, это 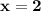$\bf{x = 2}$ .

д) Нули функции - это значения аргумента, при которых функция равна нулю. Чтобы их найти, нужно решить уравнение:

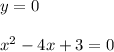
$y = 0\\\\x^2 - 4x + 3 = 0$

По теореме Виета:

$\begin{equation*}\begin{cases}x_1x_2 = 3\\x_1 + x_2 = 4\end{cases}\end{equation*}\ \ \ \ \ \Big| x = 1; x = 3$

Итак, существует два нуля данной функции: 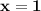$\bf{x = 1}$ и $\bf{x = 3}$ .

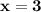е) Промежутки знакопостоянства - промежутки, на которых функция либо всегда положительна, либо всегда отрицательна. Чтобы их найти, расположим нули этой функции на координатной прямой и определим знак на каждом промежутке.

+ - +

--------------------------о--------------------------о-----------------------> x

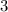
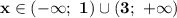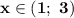Отсюда делаем вывод, что функция положительна при $\bf{x\in(-\infty;\ 1)\cup(3;\ +\infty)}$ и отрицательна при $\bf{x\in(1;\ 3)}$ .

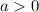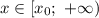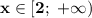ж) Когда , функция убывает при $x\in (-\infty;\ x_0]$ и возрастает при $x\in[x_0;\ +\infty)$ . Для нашего случая, функция убывает при $\bf{x\in(-\infty;\ 2]$ и возрастает при $\bf{x\in [2;\ +\infty)}$ .