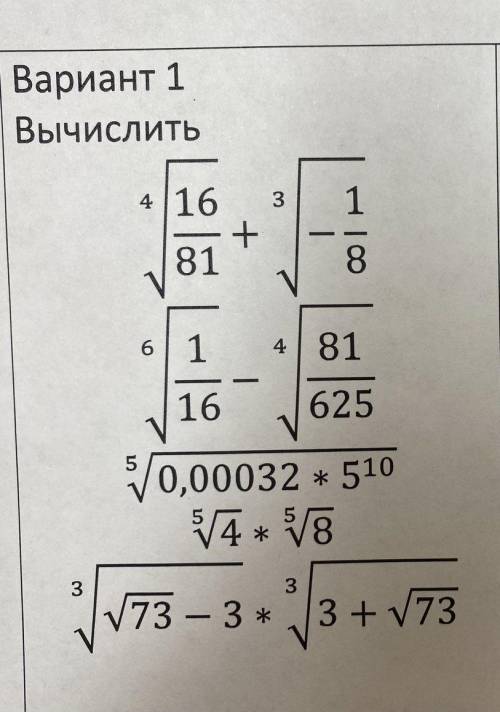
Объяснение:
![\sqrt[4]{\frac{16}{81} } +\sqrt[3]{-\frac{1}{8} } =\sqrt[4]{\frac{2^4}{3^4} }+\sqrt[3]{-\frac{1^3}{2^3} }=\sqrt[4]{(\frac{2}{3})^4 }+\sqrt[3]{(-\frac{1}{2} } )^3=|\frac{2}{3}|+(-\frac{1}{2})=\frac{2}{3}-\frac{1}{2}=\frac{1}{6} .](/tpl/images/2078/0105/50afe.png)
![\sqrt[5]{0,00032*5^{10}} =\sqrt[5]{0,2^5*5^5*5^5}= \sqrt[5]{(0,2*5)^5*5^5}=\sqrt[5]{1^5*5^5} =\sqrt[5]{5^5}=5.](/tpl/images/2078/0105/f1687.png)
![\sqrt[5]{4} *\sqrt[5]{8}=\sqrt[5]{4*8}=\sqrt[5]{32} =\sqrt[5]{2^5}=2.](/tpl/images/2078/0105/505da.png)
![\sqrt[3]{\sqrt{73} -3} *\sqrt[3]{\sqrt{73} +3} =\sqrt[3]{(\sqrt{73}-3)(\sqrt{73}+3) } =\sqrt[3]{(\sqrt{73})^2-3^2 }=\\=\sqrt[3]{73-9}=\sqrt[3]{64}=\sqrt[3]{4^3} =4.](/tpl/images/2078/0105/20dd8.png)
Изначальное неравенство:
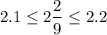
Оно нестрогое, так как скобки квадратные (данный промежуток является отрезком).
Чтобы не мучаться с неправильными дробями, вычтем из всего неравенства двойку. Так делать можно.
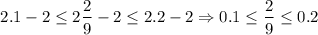
Запишем все в виде обыкновенных дробей
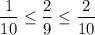
Тут вообще сразу видно, что правая часть неравенства не выполняется (это как при делении пирога: если делить его на большее количество, то каждому меньше достанется)
Чтобы не было недоразумений, докажу это:
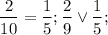
v - некоторый знак неравенства
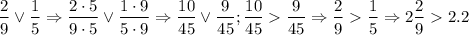
То есть наше число больше правой (большей) границы, а значит, оно НЕ принадлежит отрезку и записывается это таким образом:
![$\boxed{2\frac{2}{9}\notin [2.1; 2.2] }](/tpl/images/0305/3392/a9367.png)
здесь открыли по формуле разницы квадратов