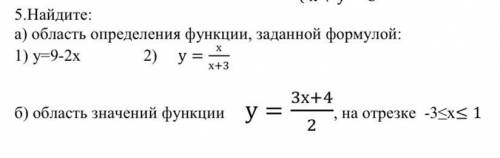
и 
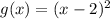. Область определения функции есть промежуток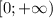 
, т.к. выражение имеет смысл только при неотрицательных значениях. Область значений функции является промежуток 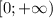. Точки построения графика: (0;0), (1;1), (4;2), (9;3).
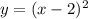является парабола, ветви направлены вверх (т.к. коэффициент при x² : а=1>0). (2;0) - координаты вершины параболы.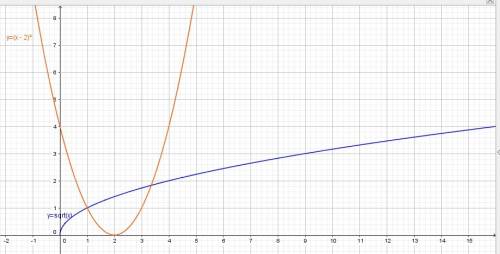
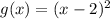и . Область определения функции есть промежуток 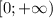, т.к. выражение имеет смысл только при неотрицательных значениях. Область значений функции является промежуток 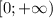. Точки построения графика: (0;0), (1;1), (4;2), (9;3). 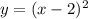является парабола, ветви направлены вверх (т.к. коэффициент при x² : а=1>0). (2;0) - координаты вершины параболы.
1) Действия по решению линейного уравнения
y=9−2x
Поменяйте стороны местами, чтобы все переменные члены находились в левой части.
9−2x=y
Вычтите 9 из обеих частей уравнения.
−2x=y−9
Разделите обе части на −2.
−2
−2x
=
−2
y−9
Деление на −2 аннулирует операцию умножения на −2.
x=
−2
y−9
Разделите y−9 на −2.
x=
2
9−y
2) Действия по решению линейного уравнения
y=
x+3
x
Переменная x не может равняться −3, так как деление на ноль не определено. Умножьте обе части уравнения на x+3.
y(x+3)=x
Чтобы умножить y на x+3, используйте свойство дистрибутивности.
yx+3y=x
Вычтите x из обеих частей уравнения.
yx+3y−x=0
Вычтите 3y из обеих частей уравнения. Если вычесть любое число из нуля, то получится его отрицательный эквивалент.
yx−x=−3y
Объедините все члены, содержащие x.
(y−1)x=−3y
Разделите обе части на y−1.
y−1
(y−1)x
=−
y−1
3y
Деление на y−1 аннулирует операцию умножения на y−1.
x=−
y−1
3y
Переменная x не может равняться −3.
x=−
y−1
3y
, x
=−3
Объяснение: Где квадратик, там перечеркнутое равно