Решите систему :
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
{xy > 0
{xz >0
{yz >0
ответ: (2 ; 2 ;2) ;
((-5-√13)/2;(-5-√13)/2;(-5-√13)/2 ) , ( (-5+√13)/2 ;(-5 +√13)/2 ;(-5+√13)/2).
Объяснение: Область Определения Системы x ≠0 ,y ≠0 , z ≠0
Очевидно( показывают три неравенство системы) , переменные системы x , y и z одного знака .
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
* * * (x/y+y/x -2) = (x²-2xy+y²) /xy = (x-y)²/xy ≥0 и т.д * * *
Удачи ! Решение во вложение
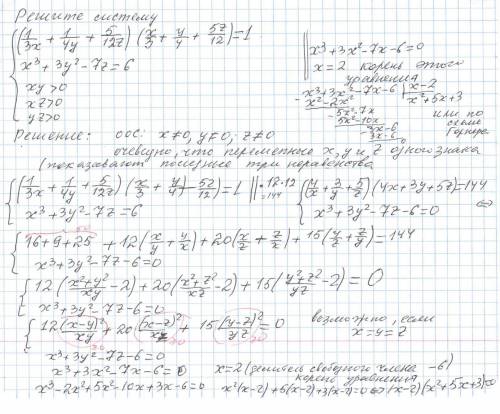
ответ: функция z имеет минимум, равный 2, в точке М(1;1).
Объяснение:
Пишем уравнение связи в виде g(x,y)=x+y-2=0 и составляем функцию Лагранжа L=z+a*g=1/x+1/y+a*(x+y-2), где a - множитель Лагранжа. Находим частные производные dL/dx и dL/dy: dL/dx=-1/x²+a, dL/dy=-1/y²*a и составляем систему из трёх уравнений:
-1/x²+a=0
-1/y²+a=0
a*(x+y-2)=0
Решая её, находим a=1, x=y=1. Таким образом, найдена единственная стационарная точка M(1;1). Теперь проверим, выполняется ли достаточное условие экстремума. Для этого находим вторые частные производные: d²L/dx²=2/x³; d²L/dxdy=0, d²L/dy²=2/y³ Вычисляем значение найденных производных в точке М: A=d²L/dx²(M)=2, B=d²L/dxdy(M)=0, C=d²L/dy²(M)=2 и составляем дифференциал 2-го порядка: d²L=A*(dx)²+2*B*dx*dy+C*(dy)²=2*dx²+2*dy²>0, поэтому функция z в точке М имеет минимум, равный zmin=1/1+1/1=2.
a^2 - b^2 = (a - b)(a + b)
|x|^2 = x^2
|x| >= 0
X^2-3|x|-5=10-5|x|
|x|^2 = x^2
|x|^2 + 2|x| - 15 = 0
D = 4 + 60 = 64
|x₁₂| = (-2 +- 8)/2 = -5 3
|x| = -5 нет |x|>=0
|x| = 3
x1 = 3
x2 = -3
|x^2+5x|-x^2=(x+2)(2-x)-5
|x^2+5x|-x^2=4 - x^2 -5
|x^2+5x| = -1
Решений нет модуль неотрицателен
|x^2-2x+4|=2|x|
|a| = |b| ⇔ a^2 = b^2
(x^2-2x+4)^2=(2x)^2
(x^2-2x+4)^2 - (2x)^2 = 0
(x^2-2x+4-2x)(x^2-2x+4+2x) = 0
(x^2 - 4x + 4)(x^2 + 4) = 0
x^2 + 4 > 0
(x - 2)^2 = 0
x = 2