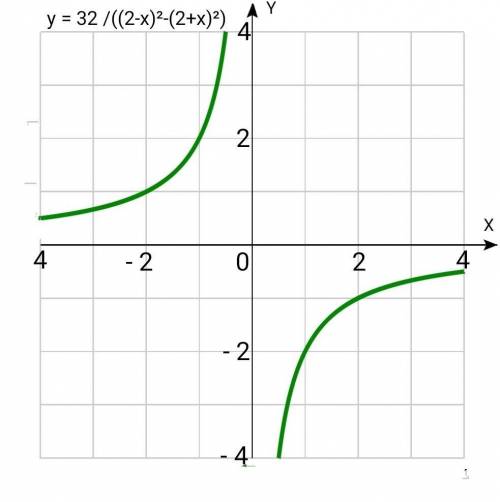
график в прикреплённом изображении.
Объяснение:
у = 32 /((2-х)²-(2+х)²)
1.
Найдём область определения функции:
выражение, записанное в знаменателе дроби, отлично от нуля,
(2-х)²-(2+х)² ≠ 0
(2-х+2+х)(2-х-2-х) ≠ 0
4•(-2х) ≠ 0
-8х ≠ 0
х ≠ 0
хє(-∞;0) ∪ (0; +∞)
2.
у = 32 /((2-х)²-(2+х)²)
у = 32 /(-8х)
у = - 4/х - обратная пропорциональность, графиком является гипербола.
Составим таблицу значений, отметим точки с указанными координатами, соединив их, получим ветви гиперболы:
х l 1 l 2 l 4 l 8 l
y l -4 l -2 l -1 l - 1/2l
Вторая ветвь гиперболы с точками, координаты которых симметричны относительно начала координат.
1)Докажите нер-во: 1. 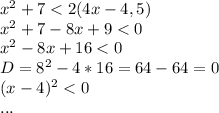
Не знаю, честно говоря что здесь требуется конкретно док-ть, прости. Т.к. тут квадрат меньше 0..
2.
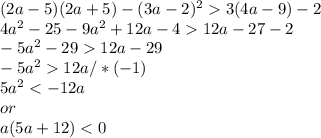
3.
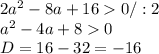
Вот тут могу док-ть и обосновать, т.к. данное квадратное ур-ие - вечный "плюс" и поэтому оно всегда будет больше 0 по определению. Вечный плюс, т.к. его дискриминант меньше 0.
2)Известно, что 7 <a <9. Оцените значение выражений:
1. a-3

2. -5a
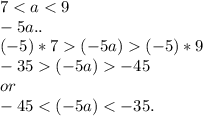
3) Дано 4 <a <3b, 2 <b <3 Оцените значение выражений: 1. а-3b
2. b-4а
3. ab
Не могу подсказать, забыла как это делать:с. Могу до утра еще исправить, если время будет. Условие я правильно записала твоих заданий?
k = - 0,5.
Объяснение нужно?