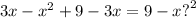
Объяснение:
x*x+x*(-3)+3x+3*(-3)
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
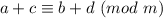
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
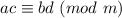
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
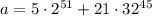
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,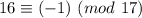 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что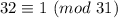 
, получаем
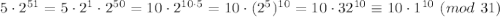
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
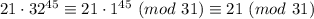
Остаток 21, чудесно. Выполняем последний шаг.
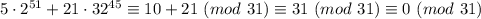
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Sn = (2*a1+(n-1)*d)*n) / 2
a1 - первый член прогрессии (у нас это 5)
d - разность прогрессии
n - количество членов, для которых мы считаем сумму.
Итак, поехали. Сначала найдем d. Для этого нужно поделить соседние члены прогрессии.
d = -10 / 5 = -2
Теперь подставляем известные нам данные в формулу, посчитаем что сможем и выразим n.
-425 = ((2*5+(n-1)*(-2))*n)/2
-425 = (10 + (-2*n+2)*n)/2
-425 = (10 -2*n^2 + 2*n)/2
- 2n^2 + 2n + 10 = -850
-2n^2+2n+10+850=0
-2n^2+2n+860 = 0
Вот и получилось у нас квадратное уравнение ;)
разделю его на - 2, чтобы проще было решать.
n^2-n-430 = 0
Теперь считаем дискриминант
D= b^2 - 4ac
a - коэффициент перед х в квадрате
b - коэффициент перед х
с - число без переменной.
D= 1 + 4*430= 1721
n = (-b2+-корень из D)/2
n1 = (1+корень из 1721)/2
n2 = (1- корень из 1721)/2
к сожалению я либо где-то обсчиталась, либо надо извлечь из корня приблизительное значение, т.к. оно ну никак не извлекается. Ошибку найти не могу, но принцип решения ясен? =)
Потом в итоге получется 2 разных n. В ответ пиши только положительное, т.к. отрицательных n не бывает.
