13+25x-x²=4x+2x+3
25x-x²-4x-2x+13-3=0
-x²+19x+10=0 |·(-1)
x²-19x-10=0
D=(-19)²-4·(-10)=361+40=401
x1=(19-√401)/2
x2=(19+√401)/2
ответ: при x=(19-√401)/2 и при x=(19+√401)/2.
Или если имелось ввиду не x², а 2x, то:
13+25x-2x=4x+2x+3
25x-2x-4x-2x=3-13
17x=-10
x=-10/17
ответ: при x=-10/17.
1) Дано: 3^(5x-2,5)≤√3, приводим к общему основанию: 3^(5x-2,5)≤3^0,5, т.к. основания одинаковые, работаем только с показателями степени и решаем неравенство: 5x-2,5≤0,5 ⇒ x≤3/5 или x≤0,6
2) Дано: (x²-1)*√(4x+7)≤0
а) Сначала выполняем ОДЗ для подкоренного выражения, которое никогда не бывает меньше нуля: 4x+7≥0 ⇒ x≥-7/4 или x≥-1,75
б) Так как всё неравенство меньше либо равно нулю, то это может быть лишь в том случае, когда x^2-1 либо меньше нуля, либо равно нулю. Зная, что произведение двух чисел равно нулю только когда оба множителя равны нулю, решим второе неравенство:
x²-1≤0, x²≤1 ⇒ x≤ 1 и x ≤ -1
в) Объедением наше решение (x≤ 1 и x ≤ -1) с ОДЗ (x≥-1,75) и получаем, что наш икс лежит в промежутке [-1,75;-1]
ответ: x∈[-1,75;-1]
3) Дано: log_2(x-2)+log_2(x)=0,5log_3(9).
Упростим его до вида: log_2(x-2)+log_2(x)=1 (в правой части получилась единица по свойству логарифмов, показатель 9 можно записать в виде 3² и степень переноситься в множитель логарифма, сокращаясь с 0,5 и в итоге получается log_3(3) либо просто один). Теперь приводим уравнение к общему основанию, логарифмируя единицу:
log_2(x-2)+log_2(x) = log_2(2), log_2(x²-2x) = log_2(2); т.к. в ообоих частях у нас получилось одинаковое основание логарифма 2, то работаем только с выражениями под логарифмом:
x²-2x=2, x²-2x-2=0, решаем как квадратное уравнение по дискриминанту: √D = √(4+8) = √12 = 2√3
Корни данного уравнения: x₁ = 2+√3 и x₂ = 2-√3
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1) 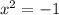
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 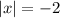
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1) 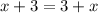
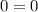
корней уравнения нет.
2) 
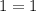
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: 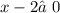 ,
, 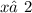 ;
;
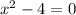
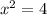
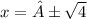
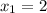 (не удовлетворяет ОДЗ),
(не удовлетворяет ОДЗ), 
ответ: 
2) 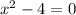
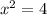
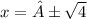
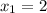 ,
, 
ответ:  ;
; 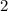
=> уравнения не равносильные.
10. 1) 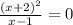
ОДЗ: 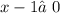 ,
, 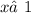 ;
;
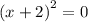
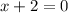

ответ: 
2) 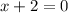

ответ: 
=> уравнения равносильные.

12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 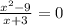
ОДЗ: 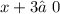 ,
,  ;
;
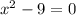


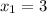 ,
,  (не удовлетворяет ОДЗ)
(не удовлетворяет ОДЗ)
ответ: 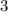
13. 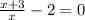
ОДЗ: 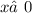 ;
;
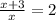
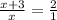
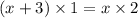
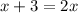
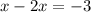
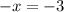
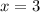
ответ: 
14. 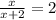
ОДЗ:  ,
,  ;
;
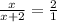
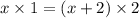

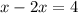


ответ: 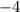
15. 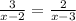
ОДЗ: 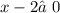 ,
, 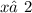 ,
, 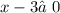 ,
,  ;
;
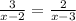
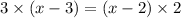
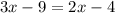
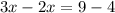
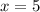
ответ: 
16. 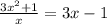
ОДЗ: 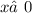 ;
;
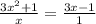
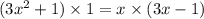
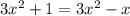
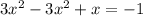

ответ: 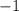
- 10/17
Объяснение:
13 + 25x - x2 = 4x + 2x + 3
25x - x2 - 4x - 2x = - 13 + 3
17x = -10
x = - 10/17