Сначала найдём косинус <A.
cos <A = AC / AB. Найдём гипотенузу AB по теореме Пифагора.
AB = √(3²+(6√6)²) = √(9 + 216) = √225 = 15 см
Теперь можно найти косинус угла A.
cos <A = 3 / 15 = 1/5 = 0.2
<1 и <A - смежные, а косинусы смежных угло противоположны по знаку.
Поэтому,
cos <1 = -0.2
Полученное значение входит в отрезок [-1;1] - других значений быть не может, значит мы всё рассчитали верно. Если бы значение косинуса угла выходило бы за этот отрезок, то это указывало бы на ошибку.
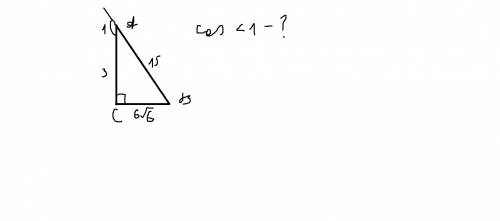
Пусть цифры числа x и y. Тогда само число, составленное из этих цифр будет равно
10x + y.(вспомните основы десятичной системы счисления).
Теперь можно записать следующие условия.
Из первого условия следует, что
10x + y - 19 = x² + y²
Из второго условия следует, что:
10x + y -9 = 10y + x. Теперь можно сосоавить систему уравнений и из неё найти цифры числа.
10x + y - 19 = x² + y²
10x + y - 9 = 10y+x
Попробуем решить систему методом подстановки. выразив из второго уравнения y:
-9y = 9 - 9x
-9y = 9(1 - x)
y = x - 1
Тогда первое уравнение запишется так:
10x + x-1 - 19 = x² + (x - 1)²
11x - 20 = x² + x² - 2x + 1
11x - 20 = 2x² - 2x + 1
2x²-13x + 21 = 0
D = b² - 4ac = 169 - 168 = 1
x1 = 13 - 1 / 4 = 12/4 = 3
x2 = 13 + 1 / 4 = 3.5 - такого ответа у нас не может быть, поскольку цифра - это всегда однозначное целое число, поэтому этот ответ можно не рассматривать.
Получаем поэтому только один вариант системы:
x = 3
y = 3 - 1 = 2
Таким образом, искомое число равно 32