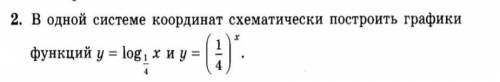
Eсли cosx > 0, т. е х в 1 и 4 четверти, делим на cosx
tgx < 1⇒ -(π/2)+πk < x < (π/4)+πk, k∈Z
Неравенству удовлетворяют корни, для которых соsx>0
Получаем
-(π/2)+2·πk < x < (π/4)+2·πk, k∈Z
Eсли cosx < 0, т. е х в 2 и 3 четверти, делим на cosx
tgx > 1⇒ (π/4)+πn < x < (π/2)+πn, n∈Z
Неравенству удовлетворяю корни, для которых соsx>0
Получаем
(3π/4)+2·πn < x < (π/2)+2·πn, n∈Z
О т в е т. Объединение ответов:
((π/2)+2·πk ; (π/4)+2·πk) U (3π/4)+2·πn ; (π/2)+2·πn), k, n∈Z
У нас есть 5 пирожков с разной начинкой. А так же есть 5 человек, 2 из которых - мальчики.
По формулам комбинаторики, число всех возможных исходов - 5 в степени 5 (кол-во пирожков в степени кол-во людей)=3125 но подходящие из низ всех лишь те, при которых вишневый пирожок достается мальчикам. Часть пирожков, которая достанется мальчикам - 2/5, то есть 1250. А из всех этих вариантов количество вишневых пирожков - 1/5, то есть 250. А значит вероятность попадания вишнёвого пирожка мальчику равняется количеству верных вариантов деленное на все варианты - 250/3125=0.08
Очень сложно для меня, сидел, мозги ломал, должно быть правильно, на этом сайте комбинаторику не любят, судя по всему)