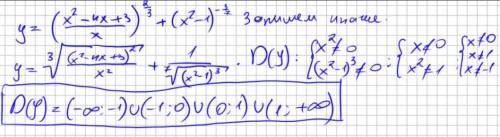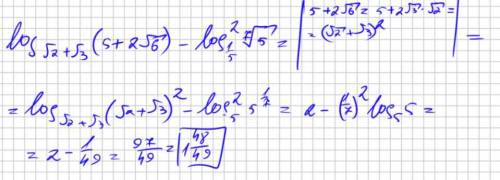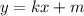 : если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором
: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 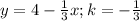 . С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения
. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 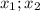 , два произвольных числа, но
, два произвольных числа, но 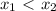 . Пусть мы имеем функцию
. Пусть мы имеем функцию  , тогда вычисляем значения функции в этих двух точках, имеем
, тогда вычисляем значения функции в этих двух точках, имеем 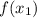 и
и 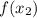 , так вот, если
, так вот, если  , тогда функция возрастающая, если же
, тогда функция возрастающая, если же 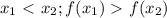 , то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)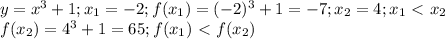 , т.е. функция возрастающая. А вот задание с
, т.е. функция возрастающая. А вот задание с 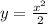 не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной)
не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 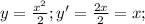 . Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка):
. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 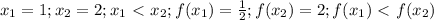 , функция возрастает, что и требовалось доказать.
, функция возрастает, что и требовалось доказать.
1) x≠-1;0;1
2) 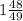
Объяснение:
8. В нахождении области определения необходимо заметить дробь и степень. Степень мы можем перевести корень, в итоге получим кубический корень который определен при любых X, поэтому в данной дроби нас волнует только знаменатель X который не должен равняться нулю. В следующем выражении видим отрицательную степень, по свойству степеней избавляемся от минуса в степени, после переводим данную степень в корень, получим корень седьмой степени, который определен при любых X, значит нас волнует только знаменатель (который образовался после применения свойства отрицательной степени). Знаменатель не должен быть равен нулю. Записываем все наши ограничения в систему и получим: 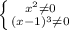 решая данную систему получим область определения. (
решая данную систему получим область определения. (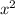 появился после преобразования степени в корень, так же и с другим выражением.)
появился после преобразования степени в корень, так же и с другим выражением.)
9. Посмотрим на число первого логарифма, и его основание. Число логарифма можно записать иначе по формуле квадрата суммы(в решении это показано), далее по свойствам логарифма, квадрат выносится, и в итоге получим два. Второй логарифм находится в квадрате, в основании 1/3, это число можно представить как 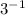 , и по свойству логарифмов вынести минус, но нужно учесть сто логарифм находится в квадрате, значит эти дейтсви можно записать так:
, и по свойству логарифмов вынести минус, но нужно учесть сто логарифм находится в квадрате, значит эти дейтсви можно записать так: ![log^{2}_\frac{1}{3}\sqrt[7]{5} =(-log_3}}\sqrt[7]{5} )^{2}=(-1^{2})*log_3 \sqrt[7]{5}=log_3 \sqrt[7]{5}](/tpl/images/4514/1609/1f559.png) , далее корень можно представить в виде степени с основание 5, и по свойству степеней вынести показатель, но при этом не забывая про квадрат логарифма.
, далее корень можно представить в виде степени с основание 5, и по свойству степеней вынести показатель, но при этом не забывая про квадрат логарифма.