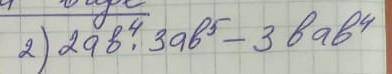
80 (л) молока в 1 бидоне.
60 (л) молока во 2 бидоне.
Объяснение:
У двох бідонах було молоко.Якщо з першого бідона перелити в другий 10 л молока то в обох бідонах молока стане порівну.Якщо з другого бідона перелити в перший 20 л молока то в першому стане у 2,5 раза більше молока ніж у другому.Скільки літрів молока було в кожному бідоні.
х - л молока в 1 бидоне.
у - л молока во 2 бидоне.
По условию задачи составляем систему уравнений:
х-10=у+10
(у-20)*2,5=х+20
Раскрыть скобки:
х-10=у+10
2,5у-50=х+20
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=у+20
2,5у-50=у+20+20
2,5у-у=40+50
1,5у=90
у=90/1,5
у=60 (л) молока во 2 бидоне.
х=у+20
х=80 (л) молока в 1 бидоне.
Проверка:
80-10=60+10
70=70
60-20=40
80+20=100
100 : 40=2,5 (раза), всё верно.
Дана функция 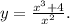
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
5ab*9=3bab*4
Объяснение:
поставь лайк