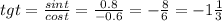Повар Миша может выполнить заказ на 136 минут быстрее, чем повар Коля.
Совместно они выполняют заказ за 51 минуту.
Пусть x минут - выполняет заказ повар Коля, тогда
x + 136 - выполняет заказ повар Миша
За 1 минуту совместной работы они выполнят 1/x + 1/(x+136) заказа.
Составим уравнение:
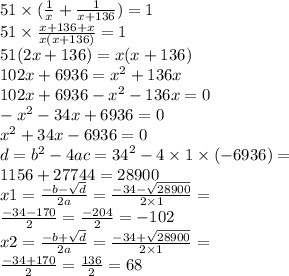
Решив данное уравнение ,получим x= - 102 и x= 68. По условию задачи x – величина положительная. Следовательно, повар Коля сможет выполнить работу за 68 минут, а повар Миша (68 + 136 = 204) за 204 минуты.
ответ: Коля выполнит заказ за 68 минут, Миша выполнит заказ за 204 минуты
cost=-0.6
1)sin²t+cos²t=1
sin²t=1-cos²t=1-(-0.6)²=1-0.36=0.64
sint=+-0.8
так как π/2 ≤ t ≤ π- 2 четверть, следовательно, там sint положительный
значит sint=0.8
2)