через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
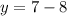
Объяснение:Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
многочлен деление пр 1
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
многочлен деление пр 1 шаг 2
Получили привычное для нас деление одночленов. Выполним это деление:
многочлен деление пр 1 решениеТаким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.
многочлен деление пр 1 решение шаг 2
надеюсь удачи здесь подробно написано
Пусть a>b>0 докажите что a³>b³, a³>ab², a⁴>a²b², a²b²>b⁴
a² - b² = (a - b)(a + b)
a³ - b³ = (a - b)(a² + ab + b²)
a>b>0 ⇒ a - b > 0 a > 0 b > 0
1. a³>b³
a³ - b³ > 0
(a - b)(a² + ab + b²) > 0 так как a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
2. a³>ab²
a³ - ab² > 0
a(a² - b²) > 0
a( a - b)(a + b) > 0 так как a и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
3, a⁴>a²b²
a⁴ - a²b² > 0
a²(a² - b²) > 0
a²(a - b)(a + b) > 0 так как a и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд
4. a²b²>b⁴
a²b²- b⁴ > 0
b²(a² - b²) > 0
b²(a - b)(a + b) > 0 так как b и a - b > 0 по условию, вторая скобка > 0 как сумма положительных чисел чтд