Преобразуйте выражения, используя законы умножения:
- 2x-3y);
а) 4а (–36);
-4(x - 2);
6) 8(2x - 3);
(3x - 1)-2.
B) (4 - x)-(-3).
Раскройте скобки и приведите
подобные слагаемые:
2x - 3+ (3x - 2);
а) х +5+ (4х – 6);
(4 - x) - (5 - 2x);
б) (3x - 2) - (5x - 8);
6 + 2(1,5х - 3).
в) 20 + 5(0,2y - 4).
8
Упростите выражение и найдите его
значение при а= -1,5:
2(a - 4) - (1 - 2a).
Докажите, что значение выражения
равно нулю при любом у:
у – 4) - 2(9y - 11) + 2.
8(2y – 5) – 4(3у – 10)
Раскройте скобки:
(b - (a + d)).
2 – (+ (z - t)).


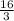
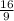
 или х₂ = 1
или х₂ = 1
Відповідь:
66 или 68
Пояснення:
Пусть х - число монет в первом столбике, тогда х+1 - во втором, х+3 - в третьем, х+n- в n-столбце
Имеем арифметическую прогрессию с начальним значением=х, d=1. n+1 елементов, тогда можем записать сумму
(2х+n)/2 ×(n+1)=2021
х=2021/(n+1) -n/2
2021=43×47 розложение на простие делители, поетому столбиков может бить 43 или 47
Значит n может равняться 42 или 46
При n=42 по формуле имеем х=26. поетому количество монет в последнем максимальном столбике = х+n=68
При n=46. х=20 тогда монет будет 66