Пусть заданное число - Х
К заданному числу прибавить его 1/3 часть: Х + 1/3*Х или Х + Х/3
то получиться число которое меньше 36 : Х + Х/3 < 36
Если данное число уменьшить на его1/2 часть: Х - 1/2*Х или Х - Х/2
то получиться число которое больше 11 : Х - Х/2 > 11
Имеем систему неравенств:
Х + Х/3 < 36
Х - Х/2 > 11
4Х/3 < 36 | * 3
Х/2 > 11 | * 2
4Х < 108 | : 4
Х > 22
Х < 27
Х > 22
ответ: 22 < Х < 27.
12 часов и 4 часа
Объяснение:
Условие.
Две снегоуборочные машины могли бы выполнить работу за 3 часа. Сколько часов потребуется для выполнения этой работы каждой снегоуборочной машине в отдельности если одна из них может выполнить всю работу на 8 часов быстрее, чем другая?
Решение.
1) Весь объём работы = 1.
2) Пусть х - время работы одной из машин на выполнение всего объёма;
тогда (х-8) - время работы другой снегоуборочной машины, которая может выполнить тот же объём на 8 часов быстрее.
3) Часовая производительность:
первой машины = 1/х;
второй машины = 1/(х-8).
4) Работая вместе 3 часа, машины выполнят весь объём работы.
(1/х + 1/(х-8)) * 3 = 1 ,
[3*(х-8+х)]/[х*(х-8)] = 1,
6х - 24 = х² - 8х,
х² - 14х +24 = 0,
х₁,₂ = 7±√(49-24) = 7±5;
х₁ = 12
х₂ = 2 - данное значение отклоняем, т.к. в таком случае получилось бы, что вторая машина работает: 2-8=-6 часов.
5) х = 12 - следовательно, первой машине потребуется для выполнения всей работы 12 часов;
х-8 = 12-8 = 4 - следовательно, второй машине потребуется для выполнения всей работы 4 часа.
ПРОВЕРКА:
(1/12 + 1/4) * 3 = 1, или 100 % , что соответствует объёму всей работы.
ответ: первой машине для выполнения всей работы потребуется 12 часов, а второй машине 4 часа.
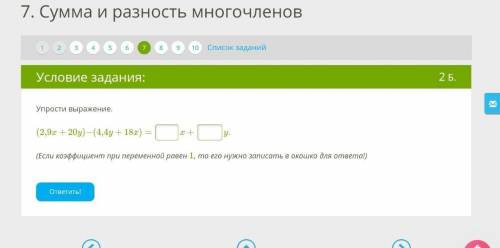
Упрощение:
2,9х+20у-4,4у-18х
ответ: -15,1х+15,6у