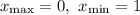Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой меняет знак с "+" на "–" (двигаясь в направлении увеличения ), то — точка максимума, а если с "–" на "+" , то — точка минимума.
Y = (1/3)*(x^3) -(x^2) Находим первую производную: f'(x) = x2-2x или f'(x) = x(x-2) Находим нули функции. Для этого приравниваем производную к нулю x(x-2) = 0 Откуда: x1 = 0 x2 = 2 На промежутке (-∞ ;0) f'(x) > 0 - функция возрастает; На промежутке (0; 2) f'(x) < 0 функция убывает; На промежутке (2; +∞) f'(x) > 0 функция возрастает. В окрестности точки x = 0 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0 - точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.
Необходимые условия экстремума:
Имеем две критические (стационарные) точки:
и 
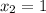
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой
меняет знак с "+" на "–" (двигаясь в направлении увеличения 
), то 
— точка максимума, а если с "–" на "+" , то 
— точка минимума.
Из промежутка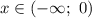
выберем, например, 
и имеем: 
Из промежутка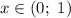
выберем, например, 
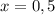и имеем: 
Имеем максимум в точке с абсциссой
Из промежутка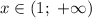
выберем, например, 
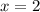и имеем: 
Имеем минимум в точке с абсциссой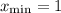
ответ: