1 область определения находим из условия 3-2х-х²≥0
-3+2х+х²≥0, по теореме, обратной теореме Виета, левая часть имеет корни х=1, х=-3, и левая часть раскладывается на линейные множители (х-1)*(х+3)≤0, мтеодом интервалов находим
____-3_______1_________
+ - +
т.е. область определения [-3;1]
Область значений - все неотрицательные действительные числа.
Наименьшее значение равно нулю.
Найдем критические точки, для чего ищем производную
f'(x)=(1/2√(3-2х-х²))*(-2x-2)
Производная равна нулю, если х=-1, Исследуем функцию на максимум, минимум и экстремум
_-3_______-1_______1_____
+ -
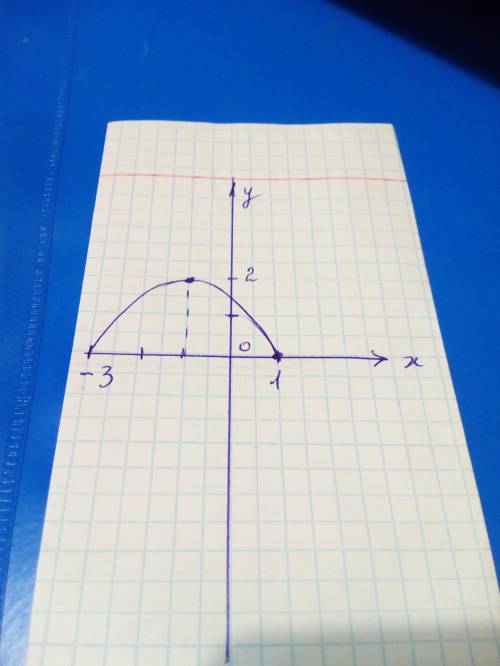
Значит, -1- точка максимума, максимум равен √(3-2*(-1)-(-1)²)=√4=2
При переходе через критическую точку знак производной меняется с плюса на минус, значит, на промежутке [-3 ;-1] функция возрастает, а на промежутке [-1 ;1] функция убывает.
График см. во вложении.
 и постройте ее график?" />
и постройте ее график?" />
ответ: В 10 классе 8 олимпиад
Объяснение:
С 7 по 11 - это 5 классов. 31:5 =6 и 1 в остатке. Т.е. в среднем, в год 6 олимпиад. Следовательно в 7 классе было меньше 6 олимпиад.
"В 11 классе количество олимпиад, в которых она приняла участие, возросло в 3 раза по сравнению с 7 классом", значит, число олимпиад в 11 классе делится на 3. Можно предположить, что это 9 или 12, тогда в 7 классе было 3 или 4 олимпиады. Проверяем:
классы: 7 8 9 10 11
количество олимпиад: 4 5 6 7 12 = 34 - это минимум при данном предположении - не подходит. Тогда остается в 7 классе - 3 и в 11 - 9 олимпиад. Получаем:
классы: 7 8 9 10 11
количество олимпиад: 3 4 5 6 9 = 27 Надо добавить еще 4. Эти 4 единицы можно добавить в 8, 9 и 10 классы. Тогда получаем:
классы: 7 8 9 10 11
количество олимпиад: 3 5 6 8 9 = 31. А по-другому распределить эти четыре единицы так, что бы "В каждом следующем учебном году она участвовала в бОльшем количестве олимпиад, чем в предыдущем" не получится. Таким образом, ответ: В 10 классе Настя приняла участие в 8 олимпиадах.
Вычёркиваем последнюю цифру 1, а затем цифру 5 и первую или третью цифру 1.
Объяснение:
Чтобы число делилось на 12, необходимо, чтобы оно делилось на 3 и на 4 одновременно (12=4*3), т.е. сумма цифр числа должна делиться на 3 и запись числа должна оканчиваться двузначным числом, делящимся на 4 без остатка.
18165121
Сначала разберёмся с признаком деления на 4. В данном случае, если зачеркнуть последнюю единицу, то запись числа будет оканчиваться двузначным числом 12, которое делится на 4.
Определим, какие две цифры ещё надо зачеркнуть, чтобы сумма оставшихся цифр делилась на 3.
Можно зачеркнуть ещё первую цифру 1 и цифру 5 или третью цифру 1 и цифру 5. Останутся два числа 18612 и 81612 Сумма цифр этих чисел 1+8+6+1+2= 8+1+6+1+2= 18, число 18 делится на 3.
Вычёркиваемые цифры выделим жирным шрифтом:
18165121
18165121