2 корня
Объяснение:
x⁴+ax²+b=0
Данное уравнение является биквадратным и должно иметь 4 корня. По условию, оно имеет три корня, т.е. три действительных корня. При b=0 это возможно.
Покажем это:
Замена: x²=y
y²+ay+b=0
При b=0 y²+ay=0
y(y+a)=0
y=0 или y+a=0
y=-a
Обратная замена: y=x²
x²=0 или x²= -a
x₁=0 x₂=√-a x₃=-√-a
Итак, уравнение x⁴+ax²+b=0 имеет три корня
При b=0 уравнение x⁴+bx²+a=0 при b=0 преобразуется в уравнение
x⁴+a=0
x⁴= -a
![x_1=\sqrt[4]{-a},\; \;\; \; x_2=-\sqrt[4]{-a}](/tpl/images/4856/7045/e2291.png)
Получаем, что это уравнение имеет два корня
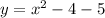
a) Найдём точки пересечения графика функции с осью ОУ. Уравнение оси ОУ: х=0.
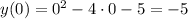
Точка пересечения графика с ОУ - точка А(0; -5) .
б) Найдём точки пересечения графика ф-ции с осью ОХ Уравнение оси ОХ: у=0.
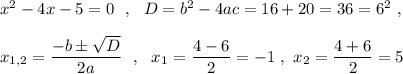
Точки пересечения графика с ОХ - точки В(1-;0) и С(5;0) .
в) Ось симметрии заданной параболы проходит через её вершину перпендикулярно оси ОХ . Найдём абсциссу вершины параболы.
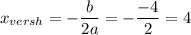
Ось симметрии - прямая х=2 .
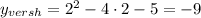, координаты вершины параболы V(2;-9) .
c) Для построения графика, можно найти координаты точки, симметричной точке А(0;-5) относительно оси х=4. Это точка D(4;-5) .
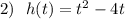
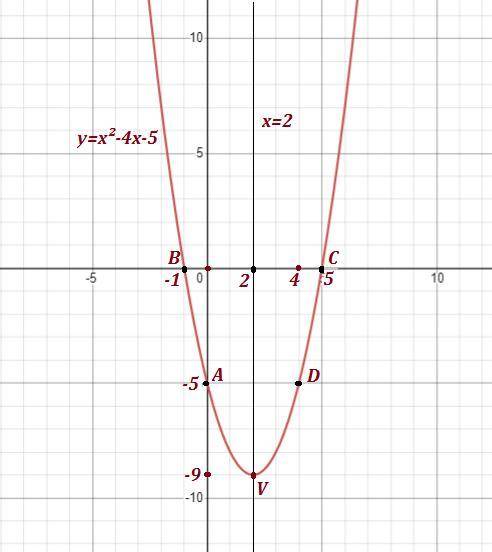
Графиком заданной функции является парабола с ветвями , направленными вверх, так как коэффициент перед t² равен 1>0 . А такая траектория движения не соответствует движению подброшенного мяча . Поэтому условие задано некорректно .
123*4=492 кг фруктов будет