Алгебра: Решите систему равнений(все на фотке)

Объяснение:Для начала разберем, что такое арифметическая прогрессия. Это такая последовательность чисел, где каждое число, начиная со второго равно предыдущему, сложенному с одним и тем же числом, то есть с разностью арифметической прогрессии. Наглядно это выглядит так:.Также существует формула - го члена арифметической прогрессии:Где - разность арифметической прогрессии.Из формулы выше, найдем разность арифметической прогрессии. Зная из условия, что , после данного числа идет девять неизвестных...

Решите систему равнений(все на фотке)

👇

Увидеть ответ

Ответ:

kalma09

11.05.2022

Объяснение:

$\left\{\begin{array}{ccc}(x+y)(x-2)=0\\(5x-6y+2)(x+5)=0\\\end{array}\right..\ \ \ \ \\$

Решим первое уравнение:

$(x+y)(x-2)=0\\x+y=0\\y=-x.\\x-2=0\\x=2.\\y=-x=-2.\ \ \ \ \Rightarrow\\x_1=2\ \ \ \ y_1=-2.\\$

Подставим значения этих корней вo второе уравнение:

$(5*2-6*(-2)+2)(2+5)=0\\(10+12+2)*7=0\\24*7=0\\168\neq 0\ \ \ \ \Rightarrow$

Эти корни не являются корнями этой системы уравнений.

Решим второе уравнение:

$(5x-6y+2)(x+5)=0\\x+5=0\\x=-5\\y=-x=-(-5)=5.\\x_1=-5\ \ \ \ y_1=5.$

Подставим значения этих корней в первое уравнение:

$(-5+5)(-5-2)=0\\0*(-7)=0\\0=0.$

Подставим значения этих корней вo второе уравнение:

$(5*(-5)-6*5+2)(-5+5)=0\\(-25-30+2)*0=0\\0=0.\ \ \ \ \ \Rightarrow$

ответ: (-5;5).

4,7(90 оценок)

Открыть все ответы

Ответ:

AnToNoVa13

11.05.2022

Центральный угол правильного многоугольника - это угол между двумя лучами, проведенными из центра многоугольника к двум его соседним вершинам. Центр правильного многоугольника совпадает с центром описанной окружности, значит, центральный угол, образованный двумя радиусами, проведенными к двум соседним вершинам, равен центральному углу многоугольника.

У правильного n-угольника n равных сторон, значит, будет n равных центральных углов.

Для двенадцатиугольника

360° : 12 = 30°

Внешний угол правильного многоугольника равен центральному углу.

Найдите центральный угол правильного двенадцатиугольника

4,4(55 оценок)

Ответ:

TEMOXAA

11.05.2022

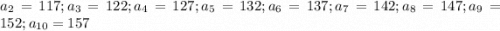
$a_{2}=117; a_{3}=122; a_{4}=127; a_{5}=132; a_{6}=137; a_{7}=142; a_{8}=147; a_{9}=152; a_{10}=157$

Объяснение:

Для начала разберем, что такое арифметическая прогрессия. Это такая последовательность чисел, где каждое число, начиная со второго равно предыдущему, сложенному с одним и тем же числом, то есть с разностью арифметической прогрессии. Наглядно это выглядит так:

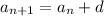$a_{n+1} =a_{n} +d$ .

Также существует формула 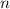- го члена арифметической прогрессии:

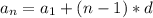
$a_{n}=a_{1} +(n-1)*d$

Где 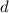- разность арифметической прогрессии.

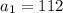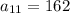Из формулы выше, найдем разность арифметической прогрессии. Зная из условия, что $a_{1} =112$ , после данного числа идет девять неизвестных чисел и последним числом будет $a_{11} =162$ .

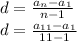
$d=\frac{a_{n}-a_{1}}{n-1}\\d=\frac{a_{11}-a_{1}}{11-1}$

Подставляем наши значения:

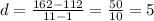$d=\frac{162-112}{11-1} =\frac{50}{10}=5$ - нашли разность арифметической прогрессии. Тогда по первой формуле мы без проблем можем найти все 9 неизвестных чисел:

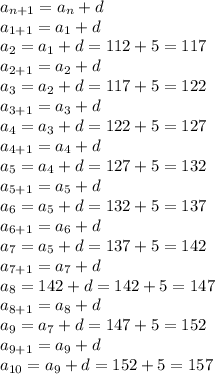
$a_{n+1} =a_{n} +d\\a_{1+1} =a_{1} +d\\a_{2} =a_{1} +d=112+5=117\\a_{2+1} =a_{2} +d\\a_{3} =a_{2} +d=117+5=122\\a_{3+1} =a_{3} +d\\a_{4}=a_{3} +d =122 +5=127\\a_{4+1} =a_{4} +d\\a_{5}=a_{4} +d =127 +5=132\\a_{5+1} =a_{5} +d\\a_{6} =a_{5} +d=132+5=137\\a_{6+1} =a_{6} +d\\a_{7} =a_{5} +d=137+5=142\\a_{7+1} =a_{7} +d\\a_{8} =142 +d=142+5=147\\a_{8+1} =a_{8} +d\\a_{9} =a_{7} +d=147+5=152\\a_{9+1} =a_{9} +d\\a_{10} =a_{9} +d=152+5=157$

Мы нашли все девять неизвестных членов арифметической прогрессии: 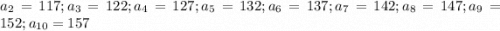$a_{2}=117; a_{3}=122; a_{4}=127; a_{5}=132; a_{6}=137; a_{7}=142; a_{8}=147; a_{9}=152; a_{10}=157$

4,5(82 оценок)

Это интересно:

Дом-и-сад

01.06.2021

Как сделать гелевый освежитель воздуха: просто, быстро и недорого...

Компьютеры-и-электроника

21.04.2022

Как победить Анкано в Skyrim...

15.01.2022

Как довольствоваться тем, что у вас есть...

Взаимоотношения

29.10.2021