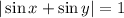Рассмотрим многочлен (функцию) f(x,c) = cx² + (c+1)x + 1. Это парабола, где с - параметр-константа.
У этого многочлена есть два корня x₁ и x₂, причем x₁<3<x₂.
Во-первых, c≠0, т.к. при с=0 будет единственный корень, т.к. при этом уравнение будет линейным.
Во-вторых, т.к. два различных корня, то D>0, то есть (c+1)² - 4·1·c > 0, ⇔
⇔ c² + 2c + 1 - 4c > 0, ⇔ c² - 2c + 1 > 0, ⇔ (c - 1)²>0, ⇔ c-1 ≠ 0, ⇔ c ≠ 1.
В-третьих, при с>0 ветви параболы будут направлены вверх, тогда область аргумента (x₁; x₂) будет иметь отрицательные значения функции, то есть условие
x₁<3<x₂ равносильно (при прочих условиях тоже) f(3,c) < 0, ⇔ c·3² + (c+1)·3 + 1 < 0, ⇔
9c + 3c + 3 + 1 < 0, ⇔ 12c < -4, ⇔ c < -4/12, ⇔ c < -1/3, что при c > 0, дает пустое множество.
В-четвертых, при c<0 ветви параболы будут направлены вниз, тогда область аргумента (x₁; x₂) будет иметь положительные значения функции, то есть условие
x₁<3<x₂ равносильно (при прочих условиях тоже) f(3,c) > 0,⇔ c·3² + (c+1)·3 + 1 > 0, ⇔
⇔ 9c + 3c + 3 + 1 > 0, ⇔ 12c > -4, ⇔ c > -4/12, ⇔ c > -1/3. Что с условием c < 0 (и другими условиями), дает в итоге -1/3<c<0, что равносильно интервалу (-1/3; 0).
ответ. (-1/3; 0).
Объяснение:
Так как функции 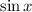 периодичные с периодом в
периодичные с периодом в 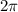 , то значения функции будут повторятся каждые
, то значения функции будут повторятся каждые
Далее без ограничений общности, можно утверждать, что от 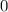 до
до 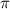 по осям х и у функция будет иметь график, в то время как для других значений из промежутка для
по осям х и у функция будет иметь график, в то время как для других значений из промежутка для ![x,y\in[-\pi;\pi]](/tpl/images/1430/8946/c0222.png) графика не будет.
графика не будет.
Тогда при 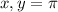 уравнение выполнено тогда, когда соответственно
уравнение выполнено тогда, когда соответственно 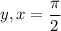 . Точно также и с 0. Для других значений из-за четности синуса будет 2 значения. Тогда график для
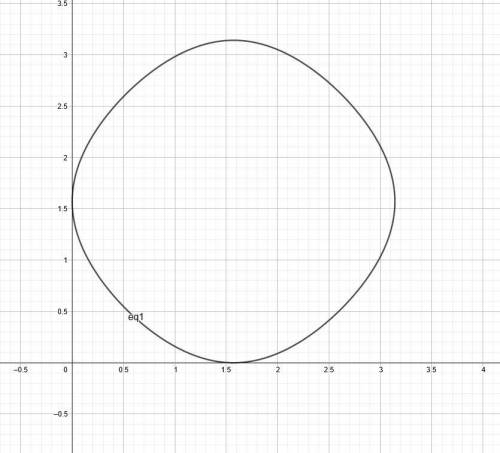
. Точно также и с 0. Для других значений из-за четности синуса будет 2 значения. Тогда график для ![x,y\in[-\pi;\pi]](/tpl/images/1430/8946/c0222.png) будет выглядеть "почти" как окружность (Но не окружность). см. рис. 1
будет выглядеть "почти" как окружность (Но не окружность). см. рис. 1
Тогда для всех х и у нам необходимо продублировать эту фигуру бесконечное число раз на 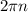 по всем осям . см. рис. 2
по всем осям . см. рис. 2
РАЗРЫВОВ НИГДЕ НЕТ!
Последняя картинка - график уравнения