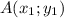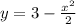. 
симметричен относительно оси 
. Пересекающая ось в точке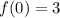 
.
.
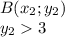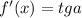. Так как график симметричен , то угол образующие касательные 
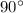, ордината будет являться биссектрисой . Следовательно треугольник будет прямоугольным и равнобедренным.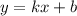 
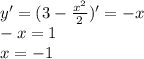, так как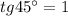 
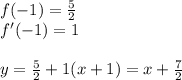
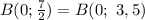
1) 10ab-5b^2-6a+3b=(10ab-5b^2)-(6a-3b)=10ab−5b
2
−6a+3b=(10ab−5b
2
)−(6a−3b)=
=5b*(2a-b)-3*(2a-b)=(2a-b)(5b-3)=5b∗(2a−b)−3∗(2a−b)=(2a−b)(5b−3)
2) a=6\frac{1}{5}=6,2;a=6
5
1
=6,2; b=2,4b=2,4
(2a-b)(5b-3)= > (2*6,2-2,4)*(5*2,4-3)=(12,4-2,4)*(12-3)=10*9=90(2a−b)(5b−3)=>(2∗6,2−2,4)∗(5∗2,4−3)=(12,4−2,4)∗(12−3)=10∗9=90
ответ: 90.