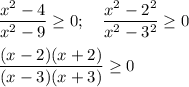
Решим неравенство методом интервалов.
Отмечаем на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. И выкалываем те, что из знаменателя. Мы получили 5 интервала. Перед дробью знак положительный и все множители имею пол. знак при х, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (все множители в нч степени - 1). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая границы.
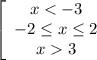
ответ: x ∈ (-∞;-3) ∪ [-2;2] ∪ (3;+∞).
В решении использовалась формула сокращённого умножения: a²-b²=(a-b)(a+b).

Найти вероятность того что пр одновременном броске двух кубиков сумма очков которые выпали равна 9?
Из трех билетов два выигрышные. Найти вероятность того что среди взятых наугад 5 билетов хотя бы один выиграшный?
Найти вероятность того что при одновременном броске двух кубиков сумма очков которые выпали равна 9?
Шесть человек случайным образом сели на лавочке. Найти вероятност ь того что два фиксированных человека будут
сидеть рядом?
Так как из трех билетов выигрышных два, то вероятность выиграть , тогда вероятность проиграть .
Зная р и q, можно найти вероятность наступления хотя бы одного события в n испытаниях по формуле: .
Подставляя известные данные, получим: .
ответ: 242/243
2) Найти вероятность того, что при одновременном броске двух кубиков сумма выпавших очков равна 9?
Всего исходов 36, благоприятных исходов 4 (выпали кубики 3/6, 4/5, 5/4, 6/3).
Тогда искомая вероятность равна отношению числа благоприятных исходов к общему числу возможных исходов: .
ответ: 1/9
3) Шесть человек случайным образом сели на лавочке. Найти вероятность того, что два фиксированных человека будут сидеть рядом?
Всего вариантов - число перестановок из 6 элементов: . Для того чтобы найти число благоприятных исходов, (то есть того, что два фиксированных человека будут сидеть рядом), мы "склеиваем" этих двоих и считаем число перестановок из 5 элементов: , но так как они могут сесть двояко (один слева, другой справа и один справа, другой слева) мы домножаем получившееся число на 2: .
Искомая вероятность равна .
ответ: 1/3