2x - y = -3; <=> y = 2x + 3. (1)
3x + y = -2; <=> y = -3x - 2. (2)
Построим графики функций (1) и (2). Координаты точки их пересечения и будут решением системы.
Функции (1) и (2) линейные, то есть их графиками являются прямые. Для построения прямой достаточно двух точек.
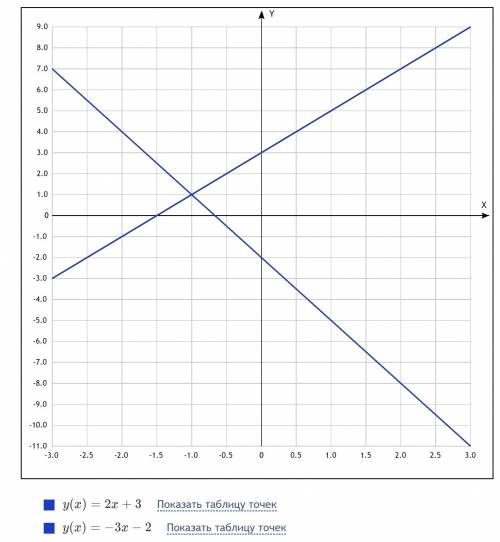
Строим график функции (1): при x = 0 y = 3; при x = 1 y = 5. Через точки (0, 3) и (1, 5) проводим прямую.
Строим график функции (2): при x = 0 y = -2; при x = -1 y = 1. Через точки (0, -2) и (-1, 1) проводим прямую.
По чертежу очевидно, что графики функций (1) и (2) пересекаются в точке (-1, 1). Следовательно, (-1, 1) - решение системы.
ответ: (-1, 1).
Чертеж:
Обьяснение:Дискриминант- то,что найти корень в квадратных уравнениях
Чтобы найти дискриминант,нужно второй коэффицент(b) возвести в квадрат и далее,отнимая 4 умножить на 1 коэффицент и на 3 коэффицент
Формула выглядит таким образом:
D=b^2-4ac
Квадратные уравнения в условий были все приведенными( коэффицент равен одному) и поэтому,в решения я не умножал на них,т.к. умножить на один= получаешь тоже самое число,по крайней мере если речь идет о положительных числах
Так же,при нахождений дискриминанта,если корень больше 0- 2 корня(нужно искать x1 и x2),если равен 0,(то 1 корень-x1),если меньше 0(нет корней,не ищешь их)
ответ:снизу
1)x2 - 4x + 4 = 0
a=1
b=-4
c=4
D=b^2-4ac
D=-4^2-4×4=16-16=0=0 1 корень
x1= 4+0/2=2
x1=2
2)
x^2 - 6x + 9 = 0
a=1
b=-6
c=9
D=-6^2-4×9=36-36=0=0 1 корень
x1=6+0/2=3
x1=3
3)
x^2 + 8x + 16 = 0
a=1
b=8
c=16
D=8^2-4×16= 64-64=0 1 Корень
x1= 8+0/2=4
x1=4
4)
x^2 - 10x + 25 = 0
a=1
b=-10
c=25
D=(-10)^2-4×25=100-100=0 1 корень
x1=10+0/2=5
x1=5
5)
x^2 - 12x + 36 = 0
a=1
b=-12
c=36
D=-12^2-4×36=144-144=0 1 корень
x1=12+0/2=6
x1=6