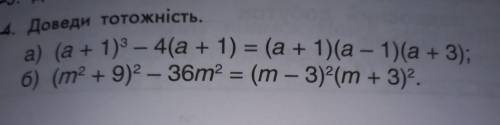
ответ:(8x + 10)(3 - x) = (11 - 2x)(4x + 5) - 5;
Раскрываем скобки, перемножая их содержимое между собой:
24х - 8х^2 + 30 - 10х = 44х + 55 - 8х^2 - 10х - 5;
Переносим все слагаемые в левую часть уравнения:
24х - 8х^2 + 30 - 10х - 44х - 55 + 8х^2 + 10х + 5 = 0;
Приводим подобные слагаемые:
- 8х^2 + 8х^2 + 24х - 10х + 10х- 44х - 55 + 30 + 5 = 0;
-20х - 20 = 0;
-20х = 20;
20х = -20;
х = -20 : 20;
х = -1.
Проверка:
(8 * (-1) + 10)(3 - (-1)) = (11 - 2 * (-1))(4 * (-1) + 5) - 5;
(-8 + 10) * 4 = (11 + 2)(-4 + 5) - 5;
2 * 4 = 13 * 1 - 5;
8 = 13 - 5;
8 = 8.
ответ: х = -1.
Объяснение:

В решении.
Объяснение:
1) В одной и той же системе координат постройте графики
функций y = x^2, y = x^3 и y = 3x + 2.
а) у = х²;
График - классическая парабола с центром в начале координат, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
По вычисленным точкам построить параболу.
б) у = х³;
График - кубическая парабола с центром в начале координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
По вычисленным точкам построить параболу.
в) у = 3х + 2;
График линейной функции прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у -1 2 5
По вычисленным точкам построить прямую.
2) Решите графически уравнение x^3 = 3x + 2.
у = х³; у = 3х + 2;
Построить графики функций и найти координаты точек их пересечения.
а) у = х³;
График - кубическая парабола с центром в начале координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
По вычисленным точкам построить параболу.
б) у = 3х + 2;
График линейной функции прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у -1 2 5
По вычисленным точкам построить прямую.
Координаты точек пересечения: (-1; -1); (2; 8).
Решения уравнения: х = -1; х = 2.