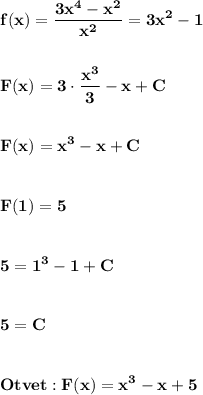
z=ln(x+e^(-y))
dz/dx=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))
d2z/dx2=((x+e^(-y))^(-1))'=-(x+e^(-y))^(-2)*(x+e^(-y))'=-1/(x+e^(-y))^2
d3z/dx2dy=(-(x+e^(-y))^(-2))'=-(-2(x+e^(-y)))^(-3)*(x+e^(-y))'=2(x+e^(-y))^(-3)*(-e^(-y))=-2e^(-y)/(x+e^(-y))^3
dz/dy=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))*(-e^(-y))=-e^(-y)/(x+e^(-y))
d2z/dydx=(-e^(-y)*(x+e^(-y))^(-1))'=-e^(-y)*((x+e^(-y))^(-1))'=
-e^(-y)*(-((x+e^(-y))^(-2)))*(x+e^(-y))'=e^(-y)/(x+e^(-y))^2
d3z/dydx2=(e^(-y)/(x+e^(-y))^2)'=e^(-y)((x+e^(-y))^(-2))'=
e^(-y)*(-2((x+e^(-y))^(-3)))*(x+e^(-y))'=-2e^(-y)/(x+e^(-y))^3
и все
-2e^(-y)/(x+e^(-y))^3-(-2e^(-y)/(x+e^(-y))^3)=-2e^(-y)/(x+e^(-y))^3+2e^(-y)/(x+e^(-y))^3=0
Объяснение:
Задача №2. Пусть Х - скорость течения реки, тогда скорость катера по течению равна (8+Х) км/ч, а против течения (8-Х) км/ч. Тогда на путь по течению он затратил 15/(8+Х) ч, а на путь против течения 15/(8-Х) ч.
Т. к. по условию на весь путь туда и обртно затрачено 4 ч, составим уравнение:
15/(8+Х) + 15/(8-Х) = 4 (приводим к общему знаменателю (8+Х) *(8-Х) = 8^2 - Х^2 = 64 - Х^2 )
(120 + 15Х + 120 - 15Х - 4(64 +Х^2) ) /64 - Х^2 = 0
система:
120 + 15Х + 120 - 15Х - 4(64 +Х^2) = 0
64 - Х^2 не равоно 0
Решаем первое ур-ние системы:
240 -256 + 4Х^2 = 0
4Х^2 = 16
Х^2 = 4
Х = 2