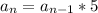
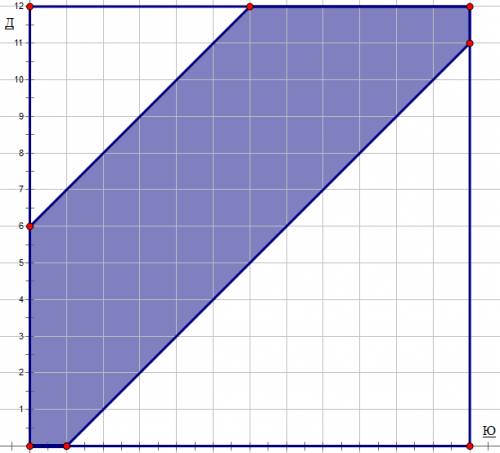
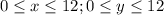. Теперь найдем, каким точкам соответствует событие "встреча состоялась". Дополнительно ко всему нижеследующему налагается условие, что точки вне квадрата не рассматриваются.
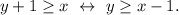. Заметим, что условие также выполняется, если юноша приходит первым, т.к. тогда правая часть отрицательна.
.
. 
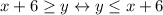В решении.
Объяснение:
Составьте квадратное уравнение, корни которого равны 5 и -2.
х₁ = 5; х₂ = -2; составить квадратное уравнение.
Уравнение вида: х² + рх + q = 0;
По теореме Виета:
х₁ + х₂ = -р; х₁ * х₂ = q;
1) Найти р:
х₁ + х₂ = -р;
5 - 2 = 3; значит, р = -3;
2) Найти q:
х₁ * х₂ = q;
5 * (-2) = -10; q = -10;
Уравнение:
х² - 3х - 10 = 0.