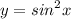
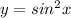
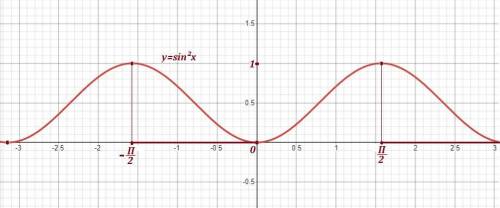
Функция убывает в тех промежутках, в которых 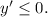
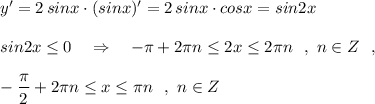
Функция убывает при ![x\in \Big[\, -\dfrac{\pi}{2}+\pi n\ ;\ \pi n\ \Big]\ \ ,\ n\in Z\ .](/tpl/images/4738/3116/bcac0.png)
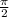 = 1
= 1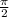 = 0
= 0 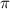 n. 2
n. 2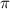 означает, что будет сделан полный оборот, и точка вернётся в тоже место, в котором была.Например выражение
означает, что будет сделан полный оборот, и точка вернётся в тоже место, в котором была.Например выражение 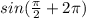 говорит нам о том, что перед тем, как искать значение
говорит нам о том, что перед тем, как искать значение  нужно "пройти" по окружности(в нашем случае против часовой стрелки, т.к. +,а не -)2
нужно "пройти" по окружности(в нашем случае против часовой стрелки, т.к. +,а не -)2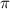 .
.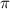 =3.14 радиан и = 180 градусам. т.е. если у нас есть +- 2
=3.14 радиан и = 180 градусам. т.е. если у нас есть +- 2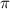 , это значит, что мы делаем ровно один круг по окружности(360 градусов).Фактически, если у тебя есть такое выражение:
, это значит, что мы делаем ровно один круг по окружности(360 градусов).Фактически, если у тебя есть такое выражение: , то ты можешь смело отбрасывать 2
, то ты можешь смело отбрасывать 2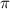 , т.к. они,фактически, не влияют на решение. Другое же дело, если у тебя стоит просто
, т.к. они,фактически, не влияют на решение. Другое же дело, если у тебя стоит просто 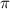 . Тогда тебе придётся перенести точку на 180 градусов, и уже к ней прибавлять угол(Пример:
. Тогда тебе придётся перенести точку на 180 градусов, и уже к ней прибавлять угол(Пример: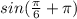 . Здесь тебе придётся перенести точку на 180 градусов и прибавить к ней угол sin
. Здесь тебе придётся перенести точку на 180 градусов и прибавить к ней угол sin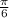 .Это будет третья четверть, а значит знак в ответе будет отрицательный(ответ:
.Это будет третья четверть, а значит знак в ответе будет отрицательный(ответ: .). Число оборотов, это n.При чём оно может быть не целым, отрицательным и т.д. но это уже совсем другая история.А вообще, наглядно это усваивается гораздо проще.Поэтому рекомендую подойти к учителю и лично попросить объяснить.
.). Число оборотов, это n.При чём оно может быть не целым, отрицательным и т.д. но это уже совсем другая история.А вообще, наглядно это усваивается гораздо проще.Поэтому рекомендую подойти к учителю и лично попросить объяснить.
Объяснение:В том случае, если катер будет двигаться против течения реки, его скорость будет равна разнице собственной скорости и скорости течения реки.
Получим:
х - 1,9 км/ч.
Если катер будет двигаться по течению реки, его скорость будет равна сумме собственной скорости и скорости течения реки.
Получим:
х + 1,9 км/ч.
Если подставить вместо значения х любое натуральное число, получим:
х = 10 км/ч.
х - 1,9 = 8,1 км/ч (скорость катера против течения реки).
10 + 1,9 = 11,9 км/ч (скорость катера по течению реки).
х - 1,9 км/ч.
(1-cos2x)/2=(1-cos²x+sin²x)/2=sin²x
Вместо функции у=sin²x рассмотрим функцию у=(1-cos2x)/2, найдем ее производную. у'=sin2x
Нас интересуют промежутки убывания, т.е. те, где у'≤0, для этого решим неравенство
sin2x≤0;
-π-arcsin0+2πn≤2х≤arcsin0+2πn ; n∈Z;
-π+2πn≤2х≤2πn ; n∈Z;
-π/2+πn≤х≤πn ; n∈Z;
ответ
х∈[ -π/2+πn; πn] ; n∈Z