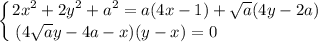
Объяснение:
1) Число 66790, А={0, 6, 7, 9} - множество цифр числа
Число 40075, В={0, 4, 5, 7} - множество цифр числа
A∩B = {0;7}
2) А - множество делителей числа 24, A={1; 2; 3; 4; 6; 12; 24}
В - множество чисел, кратных числу 6, B={6; 12; 18; 24; 30; 36;...}
A∩B = {6; 12; 24}
3) А -множество однозначный чисел (однозначные числа - это числа, состоящие из одного знака) , A={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
В- множество составных чисел, (составные числа - это натуральные числа большие 1, не являющиеся простыми числами, т.е. состоящие из произведения двух или нескольких множителей, так 4=2*2, 6=2*3, 8=2*2*2, 9=3*3, 10=2*5 и т.д.)
В={4; 6; 8; 9; 10; 12;...}
A∩B={4; 6; 8}
ОДЗ: a ≥ 0
Геометрия уравнений:
· 1-ое уравнение системы можно представить в виде
- это уравнение окружности с центром, движущимся по кривой y=√x и радиусом (a-√a)/√2.
· 2-ое уравнение - совокупность двух прямых
1) Исследуем взаимное расположение первой прямой и окружности. Подставим y = x в первое уравнение системы. Получим квадратное уравнение:
⇒ прямая y = x является касательной к окружности при любых a ≥ 0, что дает нам одно решение системы:
(!) Заметим, что при a = 0 и a = 1 окружность вырождается в точку (0, 0) и (1, 1) соответственно ⇒ система имеет только одно решение при этих значениях a.
2) Исследуем взаимное расположение второй прямой и окружности. Подставим y = (x+4a)/(4√a) в первое уравнение системы. Получим квадратное уравнение:
Оценим дискриминант при значениях a = 2, a = 3, a ≥ 4:
· a = 2
т.к. 95/66 = (99 - 4)/66 = 1.5 - (2/33) > 1.5 - (7/100) = 1.43 > √2 ≈ 1.41
· a = 3
т.к. 190/98 = (196-6)/98 = 2 - (6/98) > 2 - (7/100) = 1.93 > √3 ≈ 1.73
· a ≥ 4
- очевидно, т. к.
ведь
Таким образом, при целочисленном a ≥ 2 прямая пересекает окружность в двух различных точках и, соответственно, дает 2 решения системы. Убедимся что они не совпадают с полученным ранее решением при целочисленных a. Для этого подставим x = y = = (a + √a)/2 в уравнение y = (x + 4a)/(4√a), откуда найдем a = (33+5√41)/32 - не явл. целочисленным.
При a = 0 и a = 1 система имеет одно решение. При a ≥ 2, a ∈ Z система имеет 3 решения.
ответ: при любых целочисленных a ≥ 0.