ответ:
\frac{13k-4}{3-13k}+ \frac{x}{3-13k}=1
\frac{13k-4+x}{3-13k}= \frac{3-13k}{3-13k}
\frac{13k-4+x}{3-13k}- \frac{3-13k}{3-13k} =0
\frac{13k-4+x-(3-13k)}{3-13k}=0
\frac{13k-4+x-3+13k}{3-13k}=0
\frac{26k-7+x}{3-13k}=0
\left \{ {{26k-7+x=0} \atop {3-13k \neq 0}} \right. ; \left \{ {{x=-26k+7} \atop {k \neq \frac{3}{13} }} \right. ; \left \{ {{x=7-26k} \atop {k \neq \frac{3}{13} }} \right.
ответ: если k \neq \frac{3}{13} , то x=7-26k
объяснение:
Объяснение:
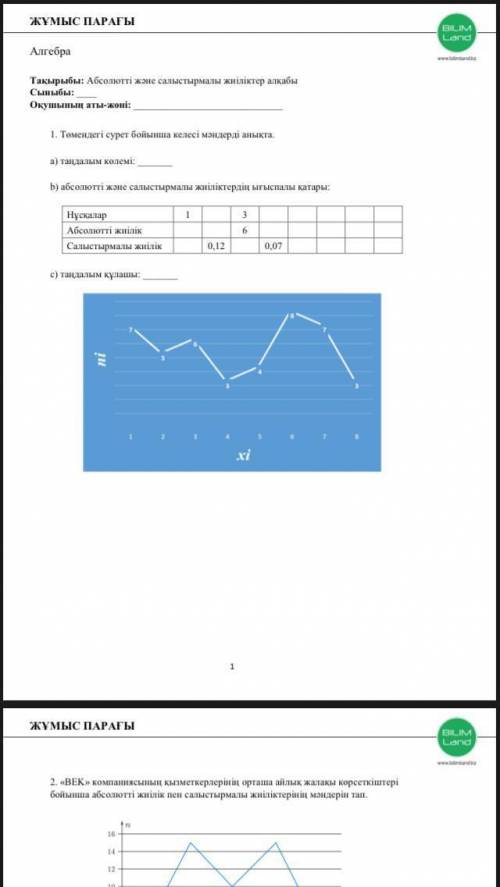
Копии | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 ||
Абсолютная частота | 7 | 5 | 6 | 3 | 4 | 8 | 7 | 3 | 43 |
Относительная частота |0,16|0,12|0,14|0,07|0,09|0,19| 0,16|0,07| 1 |.
n=7+5+6+3+4+8+7+3=43.
W=0,16+0,12+0,14+0,07+0,09+0,19+0,16+0,07=1.