
1) 3ˣ < 1 + 12·3⁻ˣ|·3ˣ; (3ˣ)² < 3ˣ + 12; (3ˣ)² - 3ˣ - 12 < 0; (3ˣ)² - 3ˣ - 12 = 0; - квадратное уравнение относительно 3ˣ, отсюда 3ˣ = 4 или 3ˣ = -3 - не имеет решений.
Рисунок во вложении
ответ: (-∞; log₃4)
2) 4·4ˣ < 7·2ˣ + 2; 4·4ˣ - 7·2ˣ - 2 < 0; 4·(2ˣ)² - 7·2ˣ - 2 = 0 - квадратное уравнение относительно 2ˣ, отсюда D = 49 + 32 = 81; √D = 9; 2ˣ = (7 + 9)/8 = 2 или 2ˣ = (7 - 9)/8 = -1/4 - не имеет решений.
Рисунок во вложении
ответ: (-∞; 1).
3) 9ˣ - 6·3ˣ - 27 = 0; (3ˣ)² - 6·3ˣ - 27 = 0; - квадратное уравнение относительно 3ˣ отсюда 3ˣ = 9; x = 2 или 3ˣ = -3 - не имеет решений.
ответ: 2.
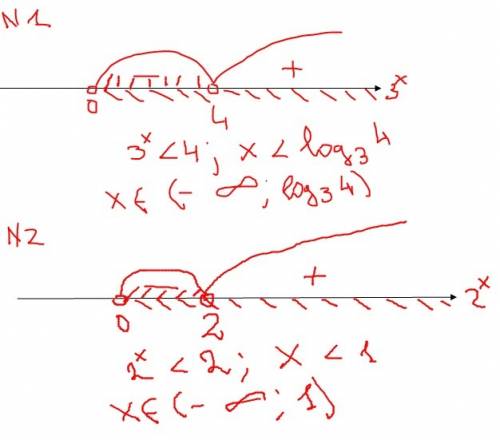
1)а) x²+3x-4=0
Коэффициенты: старший = 1
Второй = 3
Свободный член = -4
б)x²+14x=0
Коэффициенты: старший = 1
Второй = 14
Свободный член = 0
2) а)x² -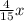 +
+ 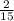 =0
=0
б)x² - 3x - 12 = 0
3) а) 0; -5
б) -3 ; 3
в) √5,5 ; -√5,5
Объяснение:
1)
a. (x-1)(x+4)=0
x²+4x-x-4=0
x²+3x-4=0
Коэффициенты: старший = a = 1
Второй = b = 3
Свободный член = c = -4
b. 12 - 6(x+3) -7x = (x-2)(x+3)
12 - 6x - 18 - 7x = x²+3x-2x-6
-6-13x = x²+x-6
-6-13x -x²-x+6=0
-x²-14x=0 (домножили на -1)
x²+14x=0
Коэффициенты: старший = a = 1
Второй = b = 14
Свободный член = c = 0
2.
a) -15x²+4x-2=0 разделим на -15
x² -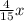 +
+ 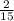 =0
=0
б) 12 - x² + 3x = 0
- x² + 3x+12=0 домножим на -1
x² - 3x - 12 = 0
3.
a) x²+5x =0
x(x+5) =0
Произведение равно 0, когда один из множителей равен 0
x1=0 или x+5=0
x2= -5
б) x² - 9 =0
x²=9
x1 = √9 = 3
x2 = -√9 = -3
в) -2x²+11=0
-2x²=-11 разделим на -2
x² = 5,5
x1=√5,5
x2= -√5,5