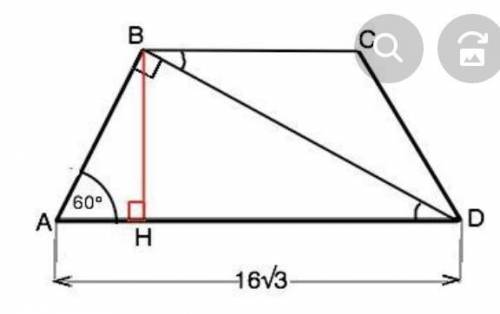
Обозначим трапецию АВСD, AB=CD, АD=16√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=8√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠ АВН=180°-90°-60°=30°. Катет АН=АВ:2=4√3. ⇒ DH=AD-AH=16√3-4√3=12√3. Высота ВН=АВ•sin60°=8√3•(√3/2)=12. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=12•12√3=144√3 (ед. площади)
==========
Как вариант решения можно доказать, что треугольник DCB - равнобедренный, ВС=CD=AB, вычислить длину высоты и затем площадь ABCD.
Объяснение:
(0;5), (10;2), (3;-6), (-4;-5), (2;9)
В каждой паре на первом месте стоит значение х ,а на втором - у.
При х=0,у=5 2x-4y=12 2*0-4*5≠12 Значит пара (0;5) не является решением уравнения.
При х=10,у=2 2*10-4*2=12 Значит пара (10;2) является решением уравнения.
При х=3,у= -6 2*3-4*(-6)≠12 Значит пара (3;-6) не является решением уравнения.
При х= -4,у= -5 2*(-4)-4*(-5)=12 Значит пара (-4;-5) является решением уравнения.
При х=2,у=9 2*2-4*9≠12 Значит пара (2;9) не является решением уравнения.
Объяснение:
1.
Вот примерно так я построил график
Красные линии - оси координат
Желтыми линиями выделены х=10 и у=0.5
При х=10 у=√10, на глаз по графику это примерно 3.2, а точно это 3.16
При у=0.5 х=0.25, тут и по графику, и вычислениями получается одинаково
2.
9=√81 - верно, точка принадлежит
0.4=√0.16 - верно, точка принадлежит
Значит ответ 3
3.
х-6=√х
х²-12х+36=х
х²-13х+36=0
d²=169-144=25=5²
x=(13±5)/2
x=9 и х=4
Проверка:
9-6=√9
3=√9 - верно
4-6=√4
-2=√4 - верно
На втором рисунке - решение графически, точка пересечения при х=9 и есть решение.
Единственное, что я не понял: почему график у=√х проходит только над осью х, ведь √х²=±х, но х=9 - это точный ответ