Алгебра: Розв язати нерівності: а)log 7(3x-5)log 5(3-2x)

Розв'язати нерівності: а)log 7(3x-5)log 5(3-2x)

👇

Ответ:

rano124

21.11.2020

A){3х-5<х+1
{3х-5>0
{Х+1>0

{3х-х<1+5
{3х>5
{x>-1

{2х<6
{x>5/3
{x>-1

{Х<3
{х>5/3
{x>-1
ответ:(5/3;3)
б){4x-3>3-2х
{4х-3>0
{3-2х>0

{4x+2x>3+3
{4x>3
{-2x>-3

{6х>6
{х>3/4
{х<1,5

{х>1
{x>3/4
{х<1,5
ответ:(1;1,5)

4,7(59 оценок)

Открыть все ответы

Ответ:

GolduckChannel

21.11.2020

Двузначное число, где а десятков и b единиц представим в виде 10a+b (это разложение числа по разрядам). Далее записываем условие задачи: 1) первое предложение

(10a+b):(a+b)=7(ост.3)

10a+b=7(a+b)+3

10a+b=7a+7b+3

3a-6b=3

a-2b=1 - это первое уравнение системы.

2) читаем второе предложение задачи

При перестановке цифр данного двузначного числа получим число 10b+a. Известно, что оно на 36 меньше, чем число 10a+b. Запишем это: 10a+b-36=10b+a

9a-9b=36 |:9

a-b=4 - это второе уравнение системы

Решаем систему:

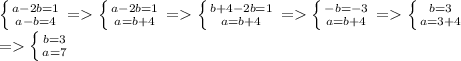
$\left \{ {{a-2b=1} \atop {a-b=4}} \right. =\left \{ {{a-2b=1} \atop {a=b+4}} \right. =\left \{ {{b+4-2b=1} \atop {a=b+4}} \right. =\left \{ {{-b=-3} \atop {a=b+4}} \right. =\left \{ {{b=3} \atop {a=3+4}} \right. \\=\left \{ {{b=3} \atop {a=7}} \right.$

Итак, искомое двузначное число равно 73.

4,4(15 оценок)

Ответ:

Аринусик111

21.11.2020

Прежде чем выполнить прологарифмирование, давайте вспомним, что такое логарифм. Логарифм это инверсия возведения в степень. То есть логарифм в основании "а" от числа "b" равен степени, в которую нужно возвести "а", чтобы получить "b". Обозначим это математическим символом:

logₐ(b) = c <=> a^c = b

Теперь применим это к нашим выражениям:

а) Прологарифмируем число 729 по основанию 3:
log₃(729) = c

Мы ищем степень, в которую нужно возвести 3, чтобы получить 729. Мы знаем, что 3^6 = 729, поэтому

log₃(729) = 6

б) Прологарифмируем число 5/6 по основанию 3:
log₃(5/6) = c

Мы ищем степень, в которую нужно возвести 3, чтобы получить 5/6. Из предыдущего примера мы знаем, что 3^6 = 729, поэтому 729/729 = 1, и 5/6 = 5/(6 * 729/729) = 5/6 * 1 = 5/6 * 729/729 = (5 * 729)/(6 * 729) = 3645/4374.

Теперь мы можем записать:

log₃(5/6) = log₃(3645/4374)

Давайте упростим это выражение:

log₃(3645/4374) = log₃(729 * 5/ (729 * 6)) = log₃(729 * 5)/log₃(729 * 6) = (log₃(729) + log₃(5))/(log₃(729) + log₃(6))

Из предыдущего примера мы знаем, что log₃(729) = 6, поэтому:

log₃(5/6) = (6 + log₃(5))/(6 + log₃(6))

в) Прологарифмируем число 1/333 по основанию 3:
log₃(1/333) = c

Мы ищем степень, в которую нужно возвести 3, чтобы получить 1/333. Мы знаем, что 1/333 можно упростить:

1/333 = 1/(3 * 111) = 1/(3 * 3 * 37) = 1/(3^2 * 37)

Теперь мы можем записать:

log₃(1/333) = log₃(1/(3^2 * 37))

Давайте упростим это выражение:

log₃(1/(3^2 * 37)) = log₃(1)/log₃(3^2 * 37) = log₃(1)/(log₃(3^2) + log₃(37))

Из предыдущего примера мы знаем, что log₃(1) = 0 и log₃(3^2) = 2, поэтому:

log₃(1/333) = 0/(2 + log₃(37)) = 0/(2 + log₃(37))

г) Прологарифмируем число ³√72 по основанию 3:
log₃(³√72) = c

Мы ищем степень, в которую нужно возвести 3, чтобы получить ³√72. Мы знаем, что ³√72 = 3^(1/3) * 3^(log₃(72)) = 3^(1/3) * 3^(log₃(3^2 * 2)) = 3^(1/3) * 3^(log₃(3^2) + log₃(2)) = 3^(1/3) * 3^(2 + log₃(2)) = 3^(1/3) * 3^2 * 3^(log₃(2)) = 3^(1/3) * 9 * 3^(log₃(2))

Теперь мы можем записать:

log₃(³√72) = log₃(3^(1/3) * 9 * 3^(log₃(2)))

Давайте упростим это выражение:

log₃(3^(1/3) * 9 * 3^(log₃(2))) = log₃(3^(1/3))/log₃(3^(log₃(2))) + log₃(9)/log₃(3) = 1/3 * log₃(3)/(log₃(2)) + log₃(9)/1 = 1/3 * 1/log₃(2) + 2/1 = 1/(3 * log₃(2)) + 2

д) Прологарифмируем число 2 по основанию 3:
log₃(2) = c

Мы ищем степень, в которую нужно возвести 3, чтобы получить 2. Мы знаем, что 3^1 = 3, поэтому:

log₃(2) = 1

Итак, проведя прологарифмирование выражений по заданному основанию 3, мы получаем следующие результаты:

а) log₃(729) = 6
б) log₃(5/6) = (6 + log₃(5))/(6 + log₃(6))
в) log₃(1/333) = 0/(2 + log₃(37))
г) log₃(³√72) = 1/(3 * log₃(2)) + 2
д) log₃(2) = 1

4,5(98 оценок)

Это интересно:

Компьютеры-и-электроника

02.01.2020

Использование Wi-Fi Direct на Android: инструкция для начинающих...

Семейная-жизнь

03.08.2021

Как избежать внематочной беременности...

Здоровье

26.08.2020

Как начать заниматься бикрам йогой...

Компьютеры-и-электроника