Формула нахождения дискриминанта применяется к выражениям формата 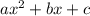 и выглядит следующим образом:
и выглядит следующим образом: 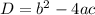 (
(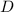 - обозначение дискриминанта).
- обозначение дискриминанта).
Для поиска корней через дискриминант используются две следующие формулы, применяемые последовательно:
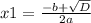
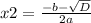
С обеих ищутся корни.
Уравнение в задании подходит под вид 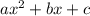 (
(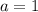 ,
, 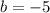 ,
, 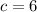 ).
).
Решим заданное уравнение через дискриминант.
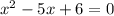
Шаг 1. Найдем дискриминант.

Шаг 2. Найдем корни уравнения.
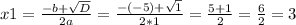
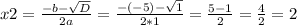
Следовательно,  имеет два значения:
имеет два значения: 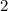 и
и 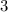 .
.
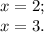
х1=3,х2=2
Объяснение:
a=1,b=-5,c=6
D=b²-4ac= 25-24=1
x1=(-b+√D): 2a= (5+1):2=3
x2=(-b-√D): 2a=(5-1):2=2