Имеем:f(x)=2x^4-x+1; f'(x)=(2x^4-x+1)'=8x^3-1
Из уравнения f'(x)=0, или 8x^3-1=0, находим стационарные точки функции f(x):
8x^3=1
x^3=1/8
x=1/2=0.5
В данном случае одна стационарная точка.
В интервал [-1, 1] попадает эта точка 1/2. В ней функция принимает значение f(1/2)=f(0.5)=2*(0.5)^4-0.5+1=5/8=0.625.
В крайних точках интервала [-1,1] имеем: f(-1) = 2*(-1)^4-(-1)+1=4; f(1)=2*1^4-1+1=2.
Из трех значений f(1/2)=f(0.5)=0.625, f(-1) =4, f(1) =2 наименьшим является 0.625, а наибольшим 4.
Поэтому минимальное значение функции f(x)=2x^4-x+1в интервале [-1,1] равно 0.625, максимальное 4.
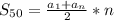- сумма арифметической пр.
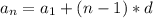- формула n-ого члена
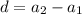- разность
или
3а1 + 3d = 234
a1 + d = 7
а2 = 7
а1 + а3 = 14
а1 = 14 - а3
По свойствам геометрической прогрессии
b1 * b3 = b2^2
b2 = a2 - 1 = 7 - 1 = 6
(14 - a3) * a3 = 6^2
a3^2 - 14a3 + 36 = 0
Получается не очень красивое число. Возможно в условии ошибка. На 1 надо уменьшать второе и третье число.
Так? Над ответом там ещё надо думать,я пока мб подумаю.