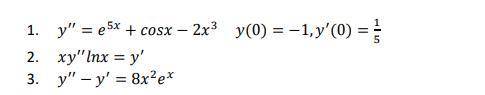
Рассмотрим систему уравнений
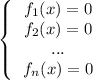
Каждое уравнение системы определяет на плоскости некоторое множество точек A1, A2, ..., An (может быть пустое или одну точку или бесконечно много точек). Решением систему уравнений называют пересечение всех этих множеств, то есть
A= A1 ∩ A2 ∩ ... ∩An.
Если
1) множество A состоит только из одной точки, то система уравнений имеет одно решение;
2) множество A пустое, то система уравнений не имеет решений;
3) множество A состоит из бесконечно много точек, то система уравнений имеет бесконечно много решений.
В частном случае можем рассмотреть систему линейных уравнений:
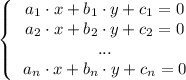
в которой, каждое из уравнений системы определяет на плоскости некоторую прямую.
Тогда возможны случаи:
1. Если все прямые совпадают, то система имеет бесконечное количество решений - так как в этом случае точек пересечений бесконечно много.
2. Если хотя бы 2 прямые системы параллельны, то есть не совпадают, то система не имеет решения - так как в этом случае нет точки пересечения.
3. Если все прямые имеют одну точку пересечения, то система имеет одно решение.
1) Интегрируем обе части: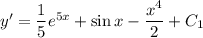 . Поскольку
. Поскольку 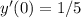 , то
, то 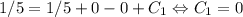 . Интегрируем еще раз:
. Интегрируем еще раз: 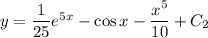 . Но поскольку
. Но поскольку 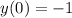 , то
, то 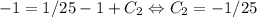 . Следовательно, ответ:
. Следовательно, ответ: 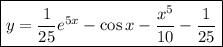
2) Сделаем замену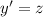 . Тогда
. Тогда 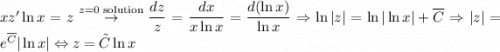
После обратной замены: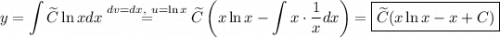
3) Здесь снова делаем замену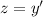 . Тогда
. Тогда 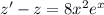 . Решаем однородное уравнение:
. Решаем однородное уравнение: 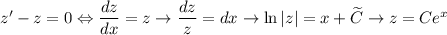 . Применяем метод вариации постоянной, то есть ищем решение в виде
. Применяем метод вариации постоянной, то есть ищем решение в виде 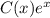 :
: 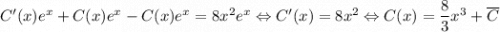 . Значит,
. Значит, 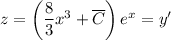 . Здесь просто интегрируем. Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная
. Здесь просто интегрируем. Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная 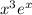 имеет вид
имеет вид 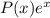 , где
, где 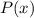 -- некоторый полином. Тогда
-- некоторый полином. Тогда 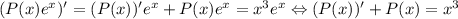 , то есть по сути, требуется решить еще один диффур, но можно поступить проще:
, то есть по сути, требуется решить еще один диффур, но можно поступить проще: 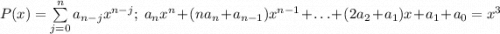 , откуда
, откуда 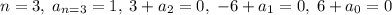 , следовательно,
, следовательно, 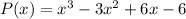 . Имеем:
. Имеем: 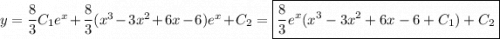 , где
, где  .
.