y = x² - 2x - 8 a = 1; b = -2; c = -8
Квадратичная функция, график - парабола, ветви направлены вверх (a=1>0). Координаты вершины :
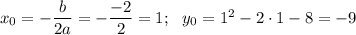
Точки для построения
x | -3 -2 -1 0 2 3 4 5
y | 7 0 -5 -8 -8 -5 0 7
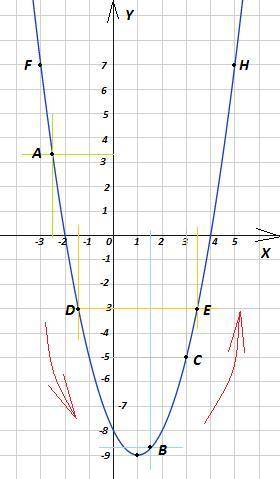
График в приложении.
a) x = -2,5; y = 3,25 Точка А
x = 1,5; y = -8,75 Точка В
x = 3; y = -5 Точка С
б) y = -3; x₁ ≈ -1,45; x₂ ≈ 3,45 Точки D и Е
y = 7; x₁ = -3; x₂ = 5 Точки F и H
в) y↑ при x ∈ [-1; +∞)
y↓ при x ∈ (-∞; 1]
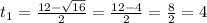

(см. объяснение)
Объяснение:
Эта строчка хорошо показывает, что аргумент логарифма есть число положительное, что избавляет от исследования ОДЗ.
Идем дальше:
Введем функцию . Это парабола, ветви которой направлены вверх. Тогда неравенство будет верно при всех
. Это парабола, ветви которой направлены вверх. Тогда неравенство будет верно при всех  , если дискриминант будет отрицательный.
, если дискриминант будет отрицательный.
Значит:
Откуда получаем, что при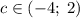 исходное неравенство выполняется для любого
исходное неравенство выполняется для любого 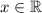 .
.
Задание выполнено!