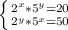 Решение задач должно содержать полное объяснение, записанное в виде последовательных логических действий, со ссылкой на математические факты, из которых следует то или иное утверждение.
Решение задач должно содержать полное объяснение, записанное в виде последовательных логических действий, со ссылкой на математические факты, из которых следует то или иное утверждение.
х = 2
у = 1
Объяснение:
I
первое уравнение равняется 20, 5^2 > 20 поэтому нам подойдет 5^1 а не 5^2 и больше, таким образом находим что х = 1.
20:5 = 4
находим первый множитель, и воспользовавшись логарифмом находим степень первого множителя.

II
5^3 > 50
5^1 нам не подойдет потому что 50:5=10 а для двойки нет такой степени которая в результате дала бы 10
поэтому нам подходит 5^2, таким образом ещё раз находим что х = 1.
50:25 =2
опять воспользовавшись логарифмом находим что у = 1.

Если изобразить эти сосны на графике - четырехугольник: сторона 14м перпендикулярна основанию (24м - расстояние между соснами), и вторая сторона 7м тоже перпендикулярна онованию.
Опускаем высоту из точки-макушки сосны 7 метров на первую сторону четырехугольника, она равна 24м (2 параллельные прямые, углы равны).
Теперь наш четырехугольник выглядит следующим образом: в основании прямогульный четырехугольник со сторонами 7м и 24м. А на нем лежит прямоугольный треугольник с катетами 24м и (14-7)м (т.е. 7м). Гипотенуза этого треугольника - искомое расстояние между макушками. Квадрат гипотенузы равен сумме квадратов катетов = 7^2+24^2 = 625
Гипотенуза = 25м
Найти вероятность того что пр одновременном броске двух кубиков сумма очков которые выпали равна 9?
Из трех билетов два выигрышные. Найти вероятность того что среди взятых наугад 5 билетов хотя бы один выиграшный?
Найти вероятность того что при одновременном броске двух кубиков сумма очков которые выпали равна 9?
Шесть человек случайным образом сели на лавочке. Найти вероятност ь того что два фиксированных человека будут
сидеть рядом?
Так как из трех билетов выигрышных два, то вероятность выиграть , тогда вероятность проиграть .
Зная р и q, можно найти вероятность наступления хотя бы одного события в n испытаниях по формуле: .
Подставляя известные данные, получим: .
ответ: 242/243
2) Найти вероятность того, что при одновременном броске двух кубиков сумма выпавших очков равна 9?
Всего исходов 36, благоприятных исходов 4 (выпали кубики 3/6, 4/5, 5/4, 6/3).
Тогда искомая вероятность равна отношению числа благоприятных исходов к общему числу возможных исходов: .
ответ: 1/9
3) Шесть человек случайным образом сели на лавочке. Найти вероятность того, что два фиксированных человека будут сидеть рядом?
Всего вариантов - число перестановок из 6 элементов: . Для того чтобы найти число благоприятных исходов, (то есть того, что два фиксированных человека будут сидеть рядом), мы "склеиваем" этих двоих и считаем число перестановок из 5 элементов: , но так как они могут сесть двояко (один слева, другой справа и один справа, другой слева) мы домножаем получившееся число на 2: .
Искомая вероятность равна .
ответ: 1/3
Разделим левую часть на левую; правую на правую. получим
(2/5)ˣ*(5/2)^(y)=20/50; после упрощения
(2/5)^(х-у)=2/5⇒х-у=1; х=у+1; подставим, например в первое уравнение, получим 2^(y+1)*5^y=20; (2*5)^y=20/2 ;10^y=10⇒ у=1, подставим в первое уравнение, получим (2)ˣ*5¹=20; 2ˣ=20/5=4=2²; х=2
ответ (2;1)
хотя ответ и прорисовывался с первого взгляда. решил досконально изложить.)