Question

решить
sin(6arcctg(-√3)+4arctg√5)

Answer 1

Формулы синуса и косинуса двойного угла:

$\sin2\alpha =2\sin\alpha \cos\alpha$

$\cos2\alpha =2\cos^2\alpha -1$

Воспользовавшись этими формулами и свойствами функции синуса, получим:

$\sin(6\,\mathrm{arcctg}(-\sqrt{3} )+4\,\mathrm{arctg}\sqrt{5})=\sin\left(6\cdot\dfrac{5\pi }{6}+4\,\mathrm{arctg}\sqrt{5}\right)=$

$=\sin(5\pi+4\,\mathrm{arctg}\sqrt{5})=\sin(\pi+4\,\mathrm{arctg}\sqrt{5})=-\sin(4\,\mathrm{arctg}\sqrt{5})=$

$=-2\sin(2\,\mathrm{arctg}\sqrt{5})\cos(2\,\mathrm{arctg}\sqrt{5})=$

$=-2\cdot2\sin(\mathrm{arctg}\sqrt{5})\cos(\mathrm{arctg}\sqrt{5})\cdot\left(2\cos^2(\mathrm{arctg}\sqrt{5})-1\right)=$

$=-4\sin(\mathrm{arctg}\sqrt{5})\cos(\mathrm{arctg}\sqrt{5})\cdot\left(2\cos^2(\mathrm{arctg}\sqrt{5})-1\right)\boxed{=}$

Найдем синус и косинус числа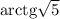 $\mathrm{arctg}\sqrt{5}$ по формулам:

$\sin(\mathrm{arctg}\,\alpha )=\dfrac{\alpha }{\sqrt{1+\alpha ^2} }$

$\cos(\mathrm{arctg}\,\alpha )=\dfrac{1}{\sqrt{1+\alpha ^2} }$

Получим:

$\sin(\mathrm{arctg}\,\sqrt{5} )=\dfrac{\sqrt{5} }{\sqrt{1+5} }=\dfrac{\sqrt{5} }{\sqrt{6} }=\sqrt{\dfrac{5}{6} }$

$\cos(\mathrm{arctg}\,\sqrt{5} )=\dfrac{1}{\sqrt{1+5} }=\dfrac{1}{\sqrt{6} }=\sqrt{\dfrac{1}{6} }$

Подставим найденные значения:

$\boxed{=}-4\cdot \sqrt{\dfrac{5}{6}}\cdot \sqrt{\dfrac{1}{6}}\cdot\left(2\cdot\left(\sqrt{\dfrac{1}{6}}\right)^2-1\right)=-\dfrac{4\sqrt{5} }{6} \cdot \left(2\cdot\dfrac{1}{6}}-1\right)=$

$=-\dfrac{2\sqrt{5} }{3} \cdot \left(\dfrac{1}{3}}-1\right)=-\dfrac{2\sqrt{5} }{3} \cdot \left(-\dfrac{2}{3}}\right)=\boxed{\dfrac{4\sqrt{5} }{9}}$