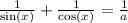
найдем дискриминант квадратного уравнения:
d = b² - 4ac = (-16)² - 4·1·48 = 256 - 192 = 64
так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
х₁ = 4, х₂ = 12
12² + (12-7)² = 13² - проверяем
144 + 25 = 169 и 13² = 169 13 больше 12 на 1, а 12 больше 5 на 7
Рассмотрим интервал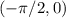 . На нем функция
. На нем функция  непрерывна. Более того, при
непрерывна. Более того, при 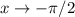 функция
функция 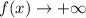 , а при
, а при 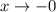 функция
функция 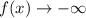 . Тогда можно выбрать такие точки
. Тогда можно выбрать такие точки  и
и 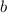 из соответственно правой и левой полуокрестностей
из соответственно правой и левой полуокрестностей 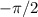 и
и 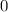 , что для заданного наперед
, что для заданного наперед 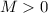 будет верно, что
будет верно, что 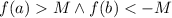 . А тогда можно применить теорему Больцано-Коши (о промежуточном значении) для отрезка
. А тогда можно применить теорему Больцано-Коши (о промежуточном значении) для отрезка ![[a,b]\subset (-\pi/2,0)](/tpl/images/4742/8553/1968d.png) и получить, что
и получить, что 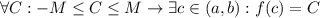 . Тогда область значений
. Тогда область значений 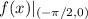 есть
есть 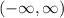 , то есть уравнение имеет решение при всех
, то есть уравнение имеет решение при всех 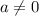 .
.