Алгебра: Доведи тотожність (x+y)³-x³=3xy(x+y); 3xy(y-x)=(x-y)³-x³+y³

Доведи тотожність (x+y)³-x³=3xy(x+y); 3xy(y-x)=(x-y)³-x³+y³

👇

Увидеть ответ

Ответ:

Chelyabin

13.03.2020

Объяснение:

(х + у)³ - х³ = 3ху(х + у)

х³ + 3х²у + 3ху² + у³ - х³ = 3х²у + 3ху²

3х²у + 3ху² + у³ = 3х²у + 3ху²

Не является тождеством

3ху(у - х) = (х - у)³ - х³ + у³

3ху² - 3х²у = х³ - 3х²у + 3ху² - у³ - х³ + у³

3ху² - 3х²у = -3х²у + 3ху²

3ху² - 3х²у = 3ху² - 3х²у

Тождественно равны

4,5(92 оценок)

Ответ:

katerinasem251

13.03.2020

1) используем формулу разности кубов слева, а³-с³=(а-с)(а²+ас+с²)

Нужно доказать. что (x+y)³-x³=3xy(x+y)

(x+y)³-x³= (x+y-x)*(х²+у²+2ху+х²+х²+ху)= y*(3х²+у²+3у)≠3xy(x+y); слева лишнее слагаемое.

нет здесь тождества.

2) Нужно доказать. что 3xy(y-x)=(x-y)³-x³+y³

распишем левую часть 3xy(y-x)=3ху²-3х²у

Распишем правую часть (x-y)³-x³+y³=х³-3х²у+3ху²-у³-х³+у³=3ху²-3х²у, поскольку левую и правую части привели к одному результату, тождество доказано.

4,7(13 оценок)

Открыть все ответы

Ответ:

vika0820

13.03.2020

Так как AK - биссектриса, то:
$\frac{BK}{AB}= \frac{KC}{AC} \ \ \textless \ =\ \textgreater \ \ \frac{BK}{KC}= \frac{AB}{AC}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
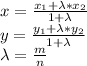
$x= \frac{x_1+\lambda*x_2}{1+\lambda}
\\y= \frac{y_1+\lambda*y_2}{1+\lambda}
\\\lambda= \frac{m}{n}$
ищем длины AB и AC:
используем формулу:
$|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
$|AB|=\sqrt{(-2-2)^2+(5-2)^2}=\sqrt{16+9}=5
\\|AC|=\sqrt{(-2-10)^2+5^2}=\sqrt{169}=13$
$\frac{BK}{KC}= \frac{AB}{AC}= \frac{5}{13} =\lambda$
находим координаты точки K:
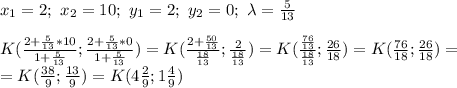
$x_1=2;\ x_2=10;\ y_1=2;\ y_2=0;\ \lambda=\frac{5}{13}
\\
\\K( \frac{2+ \frac{5}{13}*10 }{1+\frac{5}{13}} ;\frac{2+ \frac{5}{13}*0 }{1+\frac{5}{13}})=K( \frac{2+ \frac{50}{13} }{ \frac{18}{13}}; \frac{2}{ \frac{18}{13} })=K( \frac{ \frac{76}{13} }{ \frac{18}{13}}; \frac{26}{18} )=K( \frac{76}{18}; \frac{26}{18}) =
\\=K( \frac{38}{9}; \frac{13}{9})=K(4 \frac{2}{9};1 \frac{4}{9} )$
теперь определим вид треугольника для этого используем теорему косинусов:
для начала найдем длину BC:
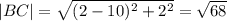
$|BC|=\sqrt{(2-10)^2+2^2}=\sqrt{68}$
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для AC и косинуса угла B
$AC^2=AB^2+BC^2-2*AB*BC*cosB
\\2*AB*BC*cosB=AB^2+BC^2-AC^2
\\cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}$
подставим значения:
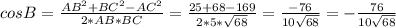
$cosB= \frac{AB^2+BC^2-AC^2}{2*AB*BC}= \frac{25+68-169}{2*5*\sqrt{68}}= \frac{-76}{10\sqrt{68}} =- \frac{76}{10\sqrt{68}}$
cosB<0 поэтому угол тупой и треугольник тупоугольный
ответ: $K(4 \frac{2}{9};1 \frac{4}{9} );\$ треугольник тупоугольный

4,4(14 оценок)

Ответ:

VIXXX

13.03.2020

У меня получилось 4 таких числа - 1236, 1248, 1296 и 1326.
Это навскидку, может и еще есть. Очевидно, первая цифра 1.
Если все цифры различны, то вторая 2 или 3.
Если вторая цифра 2, то третья не меньше 3, а последняя четная.
Если третья 3, то число делится на 2 и 3, то есть на 6. Последняя 6.
1236 делится на 2,3 и 6.
Если третья 4, то последняя 8. 1248 делится на 2, 4 и 8.
Третья не может быть 5,6,7,и 8, по разным причинам.
Если третья 9, то последняя 6, 1296 делится на 2, 9 и 6.
Если вторая 3, то получается 1326 - четное и делится на 6.

4,8(20 оценок)

Это интересно:

Хобби-и-рукоделие

25.10.2020

Как связать на спицах игрушечного медведя...

Образование-и-коммуникации

07.03.2022

Как читать показания линейки: простой гайд...

Питомцы-и-животные

27.07.2021

Как измерить температуру у лошади: советы от опытных ветеринаров и коневодов...

Дом-и-сад