Обозначим меньшую сторону прямоугольника: х см.
Тогда бо'льшая сторона: х + 7 см.
Площадь прямоугольника:
S = ab = x(x + 7) = x² + 7x.
Получили квадратное уравнение:
x² + 7x - 120 = 0 D = b²-4ac = 49 + 480 = 529 = 23²
x₁₂ = (-b±√D)/2a
x₁ = (-7-23)/2 = -15 - не удовлетворяет условию
x₂ = (-7+23)/2 = 8 (см) - меньшая сторона прямоугольника
х₂ + 7 = 8 + 7 = 15 (см) - бо'льшая сторона.
ответ: 8 см; 15 см.
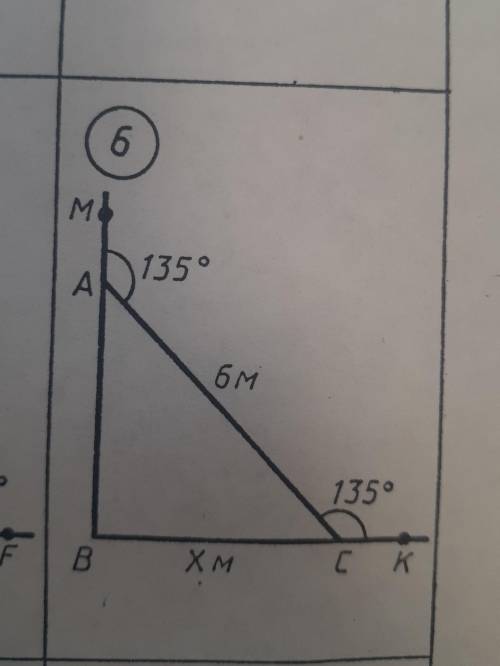
ответ:∠BAC = 180° - ∠MAC = 180° - 135° = 45° (по свойству смежных углов).
∠BCA = 180° - ∠ACK = 180° - 135° = 45° (по свойству смежных углов).
По теореме о сумме углов треугольника :
∠АВС = 180° - ∠ВАС - ∠ВСА = 180° - 45° - 45° = 90° = > ∆ABC - равнобедренный.
По теореме Пифагора :
х² + х² = 8²
2х² = 64
х² = 32
х = 4√2
ответ : 4√2 см.
Объяснение: