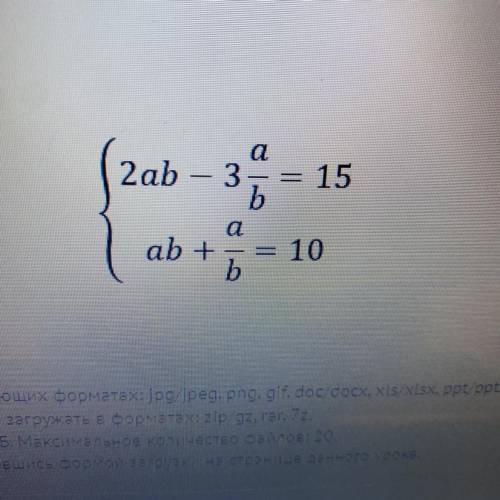
По условию задачи, дана геометрическая прогрессия bn, первые три члена которой равняются:
b1 = 5;
b2 = -10;
b3 = 20.
Найдем знаменатель q данной геометрической прогрессии. Для этого воспользуемся соотношением b2 = b1*q. Подставляя в данное соотношение значения b1 и b2 из условия задачи, получаем уравнение:
5*q = -10.
Находим q из этого уравнения:
q = -10/5;
q = -2.
Для того, чтобы убедиться, действительно ли данная последовательность является геометрической прогрессией, проверяем выполняется ли соотношение b3 = b2*q. Поскольку 20 = (-10)*(-2), то данная последовательность является геометрической прогрессией.
Находим b4:
b4 = b3*q = 20*(-2) = -40.
Находим b5:
b5 = b5*q = (-40)*(-2) = 80.
Находим теперь сумму первых пяти членов данной прогрессии:
b1 + b2 + b3 + b4 + b5 = 5 - 10 + 20 - 40 + 80 = 55.
ответ: сумма первых пяти членов данной прогрессии равна 55.
2ab - 3a/b = 15
ab + a/b = 10
Замена:
t = ab
l = a/b
2t - 3l = 15
t + l = 10
(2t - 3l) + (t + l) * 3 = 5t = 15 + 10*3 = 45
5t = 45
t = 9
l = 10 - t = 10 - 9 = 1
ab = 9
a/b = 1 ==> a = b ==> a*a=9 ==> a = b = +-3
ответ: a = b = +-3