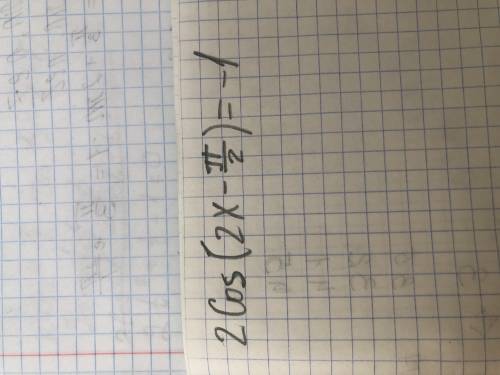
x={7/60; 11/60}, x₁+x₂=7/60+11/60=18/60=0,3
Объяснение:
sin5πx-cos5πx=√6/2
(√2/2)(sin5πx-cos5πx)=(√6/2)(√2/2)
sin(π/4)sin5πx-cos(π/4)cos5πx=√3/2
-cos(π/4+5πx)=√3/2
cos(π/4+5πx)=-√3/2
π/4+5πx=±arccos(-√3/2)+2kπ=±(π-arccos(√3/2))+2kπ=±(5π/6)+2kπ, k∈Z
1/4+5x=±5/6+2k
5x=±5/6-1/4+2k
x=±1/6-1/20+0,4k
1) x=1/6-1/20+0,4k=(7+24k)/60
0<(7+24k)/60<0,5
0<7+24k<30
-7/24<k<23/24, k∈Z⇒k=0⇒(7+0)/60=7/60
2) x=-1/6-1/20+0,4k=(-13+24k)/60
0<(-13+24k)/60<0,5
0<-13+24k<30
13/24<k<43/24, k∈Z⇒k=1⇒x=(-13+24)/60=11/60
x₁+x₂=7/60+11/60=18/60=0,3
ответ: x = (- 1 )ⁿ⁺¹• π/12 + πn/2 , nЄ Z .
Объяснение:
2cos( 2x -π/2 ) = - 1 ;
2cos( π/2 - 2x ) = - 1 ; ( функція у = соsx - парна )
cos( π/2 - 2x ) = - 1/2 ;
sin2x = - 1/2 ;
2x = (- 1 )ⁿarcsin(- 1/2 ) + πn ; nЄ Z ;
2x = (- 1 )ⁿ⁺¹arcsin( 1/2 ) + πn ;
2x = (- 1 )ⁿ⁺¹• π/6 + πn ;
x = (- 1 )ⁿ⁺¹• π/12 + πn/2 , nЄ Z .