откройте вложение, там написано решение данного задания.
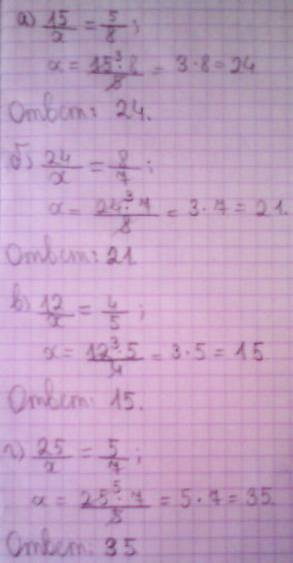
- скорость лодки.
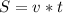
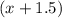км/ч. Чтобы найти расстояние, которое лодка проходит за 8 часов по течению умножаем эту скорость на 8.
- расстояние, пройденное за 8 часов по течению.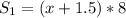
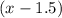км/ч. Находим расстояние, которое лодка проходит за 5 часов против течения:
. в 2 раза больше, чем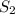 
, то есть, 
.
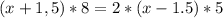
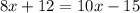
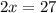
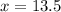(км/ч)
а)15/x=5/8
5x = 15·8
x = 3·8
x = 24
б)24/x=8/7
8x = 24·7
х = 3·7
х = 21
в)12/x=4/5
4х = 12·5
х = 3·5
х = 15
г)25/x=5/7
5х = 25·7
х = 5·7
х = 35