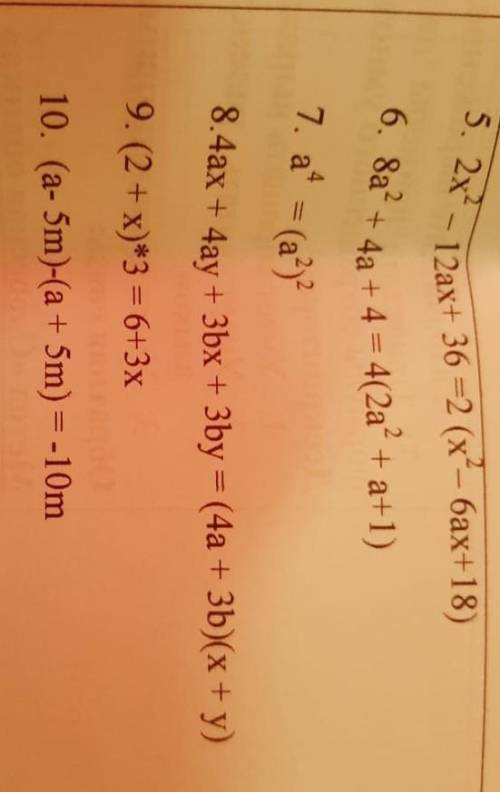
Пояснение задачи: в условии сказано: решить неравенство. Это означает, что надо найти такое множество значений для x, при котором совершается данное условие
Методы решения: в основном из одной части неравенства кидают в другое с противоположным знаком, при этом знак неравенства не меняется.
Пример:
x-5>0
x>5
Думаю, все понятно
Здесь у нас квадратичная функция, а значит у нас есть, неформально говоря, точки обрыва. Т.е. значения x, при котором уравнение 2x²+4=9x имеет решение, или попросту говоря, корни уравнения. Зачем вдруг точки обрыва - расскажу позже. А, пока, решаем квадратное уравнение:
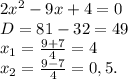
Корнями этого уравнения будут 4 и 0,5. Но, это еще не все. Мы проделали только половину пути. Решаем неравенство. Тут достаточно применить св-во, которое я описал выше:
2x²-9x+4≤0
Однако, что дальше? Да, корни наши 4 и 0,5 подходят неравенству. Но, есть еще корни, которые меньше нуля. Вот тут и играет важную роль наши "точки обрыва". Думаем логически: у нас тут явно квадратичная функция, коэффициент перед квадратом - положительный, значит ветви параболы идут вверх. График пересекает две точки: 0,5 и 4. 0,5>4. Значит то, что после 0,5 - график будет меньше 0! Да, да, меньше. И так до четверки. Множеством решений неравенства будет: x∈{0,5...4}.
Если что-то непонятно - пиши мне)
Удачи
Объяснение:
udv + vdu или udv = d(uv) - vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu (8.4.)
Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.
Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но
Объяснение:
1. 6x + 6y = 6(x + y) - да
2. ab - a^2b = ab(1 - a) ≠ ab(a - b) - нет
3. 5 - 25a^2 = 5(1 - 5a^2) - да
4. a^2 - 3a = a(a - 3) - да
5. 2x^2 - 12ax + 36 = 2(x^2 - 6ax + 18) - да
6. 8a^2 + 4a + 4 = 4(2a^2 + a + 1) - да
7. a^4 = (a^2)^2 - да
8. 4ax + 4ay + 3bx + 3by = (4a + 3b)(x + y) - да
9. (2 + x)*3 = 6 + 3x - да
10. (a - 5m) - (a + 5m) = -10m - да