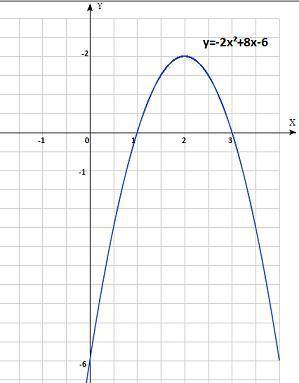
Постройте график квадратичной функции и опишите её свойства у=-2х²+8х-6
Объяснение:
у=-2х²+8х-6 ,это парабола ,ветви вниз ( -2<0).
1) Координаты вершины :
х₀=-в/2а, х₀=-8/(-2*2)=2 , у₀=-2*4+8*2-6=2, (2; 2).
2)Точки пересечения с осью ох ( у=0) ;
-2х²+8х-6 =0 , х²-4х-+3=0 , х₁=1 , х₂3 . Тогда ( 1;0) , (3;0).
3) Точки пересечения с осью оу(х=0);
у(0)=-2*0²+8*0-6 =-6 , Тогда ( 0; -6).
4) Доп.точки у=-2х²+8х-6 :
х: -1 4
у: -16 -6
Свойства функции у=-2х²+8х-6 :
а) Возрастает при х∈(-∞ ;2}, убывает при х∈[2 ;+∞).
б) Принимает положительные значения ( у>0) при х∈(1 ; 3) .
Принимает отрицательные значения (y<0) при х∈(-∞ ;1)∪(3 ;+∞).
Принимает значения равные нулю ( у=0) при х=1, 3.
в) Принимает наибольшее значение у=2 при х=2.
0,5х-2у=0 х-у-3=0
0,5х=2у у=х-3
у=0,25х
Теперь подставляем вместо х любое число,находим у и строим графики.Например:
0,25*0=0 (х=0,у=0)
0,25*4=1 (х=4,у=1) и т.д.
Так же и со вторым уравнением:
0-3=-3 (х=0,у=-3)
5-3=2 (х=5,у=2) и т.д.
Когда построите эти графики,они пересекуться в точке(4;1).Можно доказать это и по другому.Приравняем правые части наших уравнений:
0,25х=х-3
х-0,25х=3
0,75х=3
х=4
Подставим это значение в наши уравнения и найдем у:
0,25*4=1 и 4-4=1, т.е. у в обоих случаях=1
ответ: (4;1)