Приравняем выражения ⇒ 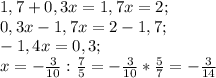
Объяснение:
№89
∠СDA = 90°, т.к. Вписанный угол, опирающийся на диаметр, является прямым углом. Следовательно,
ΔСDA - прямоугольный. Сумма всех углов = 180°. Значит,
∠DAC = 180° - 90° - 54° = 36°
∠ВАD = ∠DAC +∠САВ, откуда
∠САВ = ∠ВАD - ∠DAC = 78°-36° =42°
∠САВ = 42°
№ 90
1) Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами, т.е.
∠α = ½ ∪АВ, откуда
∪АВ = 2∠∝
α = 40° → β = 80° (1а ) → α + β =120° (1с )
α = 70° → β = 140° (2с) α + β =210°
α = 80° → β = 160° (3d) α + β = 240° (3b)
ответ: 1а, 1 с
2с
3d, 3b
Приравняем многочлены (x + 1)^2 и 7x - 3x^2, и решим получившееся уравнение.
(x + 1)^2 = 7x - 3x^2 - раскроем скобку, применив формулу квадрата двучлена (a + b)^2 - a^2 + 2ab + b^2, где a = x, b = 1;
x^2 + 2x + 1 = 7x - 3x^2 - перенесем слагаемые из правой части уравнения в левую; при переносе слагаемых из одной части уравнения в другую, знаки переносимых слагаемых меняются на противоположные;
x^2 + 2x + 1 - 7x + 3x^2 = 0;
(x^2 + 3x^2) + (2x - 7x) + 1 = 0;
4x^2 - 5x + 1 = 0;
D = b^2 - 4ac;
D = (-5)^2 - 4 * 4 * 1 = 25 - 16 = 9; √D = 3;
x = (-b ± √D)/(2a);
x1 = (5 + 3)/(2 * 4) = 8/8 = 1;
x2 = (5 - 3)/8 = 2/8 = 1/4.
ответ. 1; 1/4.
Объяснение: