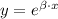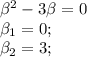
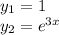
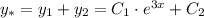
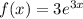
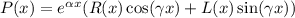.
, где R(x) и S(x) - полиномы, которое имеет частное решение.
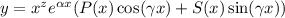, где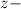 
кратность корня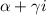 
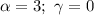
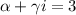является корнем характеристического уравнения кратности z=1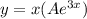
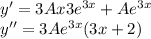
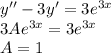
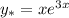
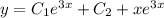
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
Дано: ABCD, AD║ BC, AD = BC.
Доказать: ABCD - параллелограмм.
Доказательство:
Проведем BD.
ВС = AD по условию,
∠1 = ∠2 как накрест лежащие при пересечении AD║BC секущей BD,
BD - общая сторона для треугольников ABD и CDB, ⇒
ΔABD = ΔCDB по двум сторонам и углу между ними.
Из равенства треугольников следует, что
∠3 = ∠4, а это накрест лежащие углы при пересечении прямых CD и АВ секущей BD, значит
CD║AB.
Если в четырехугольнике противоположные стороны параллельны, то это параллелограмм.
2 признак.
Если в четырехугольнике противоположные стороны равны, то этот четырехугольник - параллелограмм.
Дано: ABCD, AB = CD, BC = AD.
Доказать: ABCD - параллелограмм.
Доказательство:
Проведем BD.
ВС = AD по условию,
AB = CD по условию,
BD - общая сторона для треугольников ABD и CDB, ⇒
ΔABD = ΔCDB по трем сторонам.
Из равенства треугольников следует, что
∠1 = ∠2, а это накрест лежащие углы при пересечении прямых ВС и AD секущей BD, значит ВС║AD и ABCD - параллелограмм по первому признаку.
3 признак.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
Дано: ABCD, AC∩BD = O, AO = OC, BO = OD.
Доказать: ABCD - параллелограмм.
Доказательство:
AO = OC по условию,
BO = OD по условию,
∠АОВ = ∠COD как вертикальные, ⇒
ΔАОВ = ΔCOD по двум сторонам и углу между ними.
Значит, AB = CD и ∠1 = ∠2, а это накрест лежащие углы при пересечении прямых АВ и CD секущей АС, значит АВ║CD.
ABCD - параллелограмм по первому признаку.
1) x^4-10x^2+25=(x^2)^2-2x^2*5+5^2=(x^2-5)^2
2) b^4-6b^2+9=(x^2)^2-2b^2*3+3^3=(b^2-3)^2.
Формулы:
(a-b)^2=a^2-2ab+b^2