Задания: 1 Б.
Дракон, который сидел в пещере и охранял сокровища, через некоторое время согласился выплачивать
процент жителям города, которые подрядились оберегать его сон, поскольку сокровищ было несметное
количество, а дракона без конца беспокоили экспедиции кладоискателей. Хороший же сон обеспечил бы
дракону возможность периодически грабить другие сокровищницы и приумножать горы золота. Проценты
стали начисляться со дня, в который это решение было принято, до срока, когда стороны решат расторгнуть
договор. Проценты эти жители города договорились периодически забирать, для того чтобы покупать хорошие
дубовые доски для изготовления мебели, которой славился город. 1 января 20950 года был заключён этот
договор. Сокровища в пещере были оценены сторонами в размере 1,6 млн золотых, а процент, который дракон
согласился отдавать, был равен 4% в год от суммы оценки, срок договора определили немалый — 56 лет (год).
Причитающиеся проценты можно будет забирать первого числа каждого следующего месяца.
Смогут ли мастера купить досок в июле 20952 года на сумму 79 тыс. золотых, если сделать это они могут только
на проценты от сокровища? (В ответе укажи возможность или невозможность покупки и сумму, которые жители
города получат к этому сроку. ответ округли до тысяч.)
купить доски.
ответ:
тысяч золотых получат жители города и
ответить
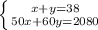
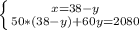
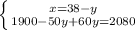
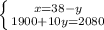
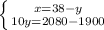

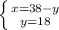
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .
sin(arcsin x) = x
arcsin(sin x) = x
Арксинус иногда обозначают так:
График функции арксинус.
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccosАрккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений .
cos(arccos x) = x
arccos(cos x) = x
Арккосинус иногда обозначают так:
График функции арккосинус.
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
ЧетностьФункция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
Свойства - экстремумы, возрастание, убываниеarccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Основные свойства арксинуса и арккосинуса представлены в таблице.
y = arcsin xy = arccos xОбласть определения– 1 ≤ x ≤ 1– 1 ≤ x ≤ 1Область значений Возрастание, убываниемонотонно возрастаетмонотонно убываетМаксимумы Минимумы Нули, y = 0x = 0x = 1Точки пересечения с осью ординат, x = 0y = 0y = π/2Таблица арксинусов и арккосинусовВ данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
xarcsin xarccos xград.рад.град.рад.– 1– 90°– 180°π– – 60°– 150°– – 45°– 135°– – 30°– 120°00°090°30°60°45°45°60°30°190°0°0≈ 0,7071067811865476
ФормулыСм. также:≈ 0,8660254037844386
Вывод формул обратных тригонометрических функций
Формулы суммы и разностипри или
при и
при и
при или
при и
при и
при
при
Выражения через логарифмы, комплексные числаСм. также:при
при
Вывод формул
Выражения через гиперболические функции
Производные;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков:
Интегралы,
где – многочлен степени . Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Делаем подстановку x = sin t и интегрируем по частям:
.
Выразим арккосинус через арксинус:
Разложения в ряды.
При |x| < 1 имеет место следующее разложение:
Обратные функции;
.
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .